
���� ��1����ϸ���⣬�ɹ㰲�г���ļƼ۱����ܹ��г��˿ʹ��һ��B������ķ���f��x����Ԫ����ʾΪ�г�x��0��x��60����λ��km���ķֶκ�����
��2��ֻ��һ�����ij���Ϊ��f��16��=2.85��16-5.3=40.3Ԫ������2�����ij���Ϊ��2f��8��=2����4.2+1.9��8��=38.8Ԫ���ɴ��ܵõ��ó˿ͻ��˱�ֻ��һ������ʡǮ��
��� �⣺��1��������ã�����f��x������·��x�ĺ���Ϊ��
f��x��=$\left\{\begin{array}{l}{8��0��x��2}\\{8+.9��x-2����2��x��10}\\{8+1.9��8+2.85��x-10����10��x��20}\end{array}\right.$=$\left\{\begin{array}{l}{9��0��x��2}\\{8+1.9x��2��x��10}\\{2.85x-5.3��10��x��20}\end{array}\right.$��
��2��ֻ��һ�����ij���Ϊ��f��16��=2.85��16-5.3=40.3��Ԫ������
����2�����ij���Ϊ��2f��8��=2����4.2+1.9��8��=38.8��Ԫ������40.3��38.8��
��ó˿ͻ��˱�ֻ��һ������ʡǮ��
���� ���⿼��ֶκ���������ʵ���е�Ӧ�ã�����ʱҪ�������⣬ע���ھ������е����������������ؽ��еȼ�ת����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | $2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
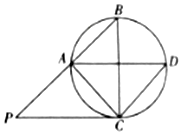 ��ͼ����P�ǡ�ABC���ԲԲO��C�������������AB�Ľ��㣮
��ͼ����P�ǡ�ABC���ԲԲO��C�������������AB�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
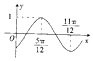 ��֪����f��x��=sin����x+�գ����أ�0���У�|��|����2�У��IJ���ͼ����ͼ��ʾ����յ�ֵΪ��������
��֪����f��x��=sin����x+�գ����أ�0���У�|��|����2�У��IJ���ͼ����ͼ��ʾ����յ�ֵΪ��������| A�� | $\frac{5��}{3}$ | B�� | $\frac{4��}{3}$ | C�� | -$\frac{4��}{3}$ | D�� | -$\frac{5��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3 | B�� | ��$\frac{9}{2}$ | C�� | 3 | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=\root{3}{x^3}$ | B�� | $y={��\sqrt{x}��^2}$ | C�� | $y=\sqrt{x^2}$ | D�� | $y=\frac{x^2}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
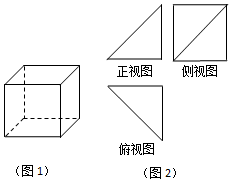
| A�� | $\frac{4}{3}$ | B�� | $\frac{8}{3}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com