【题目】一种密码锁的密码设置是在正
边形
的每个顶点处赋值0和1两个数中的一个，同时，在每个顶点处染红、蓝两种颜色之一，使得任意相邻的两个顶点的数字或颜色中至少有一个相同.问：该种密码锁共有多少种不同的密码设置？
【答案】当
为奇数时，有
种；当为偶数时，有
种.
【解析】
对于该种密码锁的一种密码设置，若相邻两个顶点上所赋值的数字不同，则在它们所在的边上标上
；若颜色不同，则标上
；若数字和颜色都相同，则标上
.于是，对于给定的点
上的设置（共有4种），按照边上的字母可以依次确定点
上的设置.为了使得最终回到时的设置与初始时相同，标有和的边都是偶数条.
所以，这种密码锁的所有不同的密码设置方法数等于在边上标记、、使得标有和的边都是偶数条的方法数的4倍.
设标有的边有
（
）条，标有的边有
（
）条.
选取条边标记的有
种方法，在余下的边中取出条边标记的有第
种方法，其余的边标记.
由乘法原理知共有
种标记方法.
对
、
求和，密码锁的所有不同的密码设置方法数为
. ①
这里，约定
.
当为奇数时，
，此时，
. ②
代入式①中得
.
当为偶数时，若
，则式②仍然成立；若
，则正边形的所有边都标记，此时，只有一种标记方法.于是，所有不同的密码设置的方法数为
.
综上，这种密码锁的所有不同的密码设置方法数是：当为奇数时，有种；当为偶数时，有种.
科目：高中数学 来源： 题型：
【题目】下表是一个“数阵”：
1 | （ ） | （ ） | （ ） | … |
| … |
（ ） | 1 | （ ） | （ ） | … |
| … |
（ ） | （ ） | （ ） | 1 | … |
| … |
… | … | … | … | … | … | … |
|
|
|
| … |
| … |
… | … | … | … | … | … | … |
其中每行都是公差不为0等差数列，每列都是等比数列，
表示位于第i行第j列的数.
（1）写出
的值：
（2）写出的计算公式，以及第2020个1所在“数阵”中所在的位置.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足：an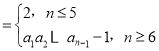
（n∈N*）．若正整数k（k≥5）使得a12+a22+…+ak2＝a1a2…ak成立，则k＝（ ）
A.16B.17C.18D.19
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
(1)用分段函数的形式表示函数f(x)；
(2)在平面直角坐标系中画出函数f(x)的图象；
(3)在同一平面直角坐标系中，再画出函数g(x)＝
(x>0)的图象(不用列表)，观察图象直接写出当x>0时，不等式f(x)> 的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
的离心率为2，过点
、斜率为1的直线
与双曲线
交于
、
两点且
，
.
（1）求双曲线方程。
（2）设
为双曲线右支上动点，
为双曲线的右焦点，在
轴负半轴上是否存在定点
，使得
？若存在，求出点的坐标；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且cosA=
，cosB=
.
（1）求sinC的值；
（2）若a-b=4-2
，求△ABC的面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于数列
，若
，则称数列为“广义递增数列”，若
，则称数列为“广义递减数列”，否则称数列为“摆动数列”.已知数列
共4项，且
，则数列是摆动数列的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
