已知函数f(x)=x3-3ax(a∈R),函数g(x)=㏑x.
(1)当a=1时,求函数f(x)在区间[-2,2]上的最小值;
(2)若在区间[1,2]上f(x)的图象恒在g(x)的图象的上方(没有公共点),求实数a的取值范围;
(3)当a>0时,设h(x)=|f(x)|,x∈[-1,1].求h(x)的最大值F(a)的解析式.
解:(1)∵f'(x)=3x
2-3=0,∴x=±1
∵f(-2)=-2,f(2)=2,f(1)=-2
∴函数的最小值为f(x)
min=-2
(2)∵在区间[1,2]上f(x)的图象恒在g(x)图象的上方
∴x
3-3ax≥lnx在[1,2]上恒成立得
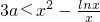
在[1,2]上恒成立
设h(x)=
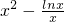
则
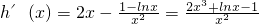
∵2x
3-1≥0,lnx≥0
∴h'(x)≥0
∴h(x)
min=h(1)=1
∴

(3)因g(x)=|f(x)|=|x
3-3ax|在[-1,1]上是偶函数,故只要求在[0,1]上的最大值
①当a≤0时,f′(x)≥0,f(x)在[0,1]上单调递增且f(0)=0,∴g(x)=f(x)F(a)=f(1)=1-3a.
②当a>0时,
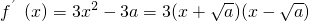
,(ⅰ)当
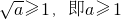
g(x)=|f(x)|=-f(x),-f(x)在[0,1]上单调递增,此时F(a)=-f(1)=3a-1
(ⅱ)当
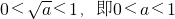
时,
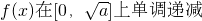
,在
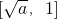
单调递增;
1°当
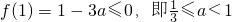
时,
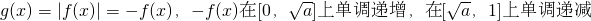
,
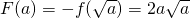
;
2°当
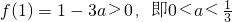
(ⅰ)当
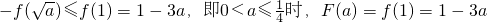
(ⅱ)当
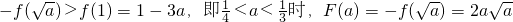
(1)-2
∴F(a)=
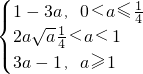
分析:(1)求出函数的导数,再通过列表得出导数的正负与单调性的规律,得出函数在区间[-2,2]上的最小值为f(-2)和f(1)中的较小的函数值;
(2)转化为不等式
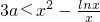
在区间[1,2]上恒成立,变成求右边函数在区间[1,2]上的最小值问题,通过讨论导数的符号,得到3a≤1,从而求得a的取值范围;
(3)首先发现函数h(x)为偶函数,故只需求h(x)在[0,1]上的最大值.然后根据参数a的取值范围,分别讨论函数h(x)在区间[0,1]上的单调性,从而得到函数h(x)在区间[0,1]上的最大值F(a)的解析式.
点评:本题以函数为载体,考查利函数的单调性,函数的最值,用导数工具讨论函数的单调性,是求函数的值域和最值的常用方法.本题还考查了分类讨论思想在函数题中的应用,同学们在做题的同时,可以根据单调性,结合函数的草图来加深对题意的理解.

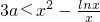 在[1,2]上恒成立
在[1,2]上恒成立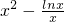 则
则 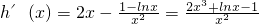

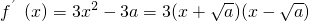 ,(ⅰ)当
,(ⅰ)当 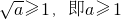 g(x)=|f(x)|=-f(x),-f(x)在[0,1]上单调递增,此时F(a)=-f(1)=3a-1
g(x)=|f(x)|=-f(x),-f(x)在[0,1]上单调递增,此时F(a)=-f(1)=3a-1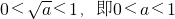 时,
时,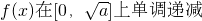 ,在
,在 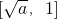 单调递增;
单调递增;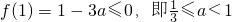 时,
时,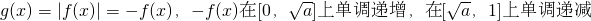 ,
,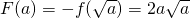 ;
;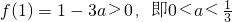
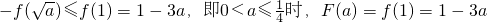
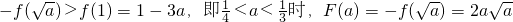 (1)-2
(1)-2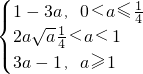
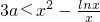 在区间[1,2]上恒成立,变成求右边函数在区间[1,2]上的最小值问题,通过讨论导数的符号,得到3a≤1,从而求得a的取值范围;
在区间[1,2]上恒成立,变成求右边函数在区间[1,2]上的最小值问题,通过讨论导数的符号,得到3a≤1,从而求得a的取值范围;

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<