分析:第①个命题说明回归直线通过样本中心点.
②:由幂函数的概念判断出m
2-m-1等于1;列出等式求出m,再根据象关于y轴对称验证其指数为偶数.再判断其单调性;
③:先利用导数求出函数
f(x)=ax3-bx2+ax+π在R上有两个相异极值点的充要条件,得出关于a,b的约束条件,在a-o-b坐标系中画出可行域,再利用几何概型求出两者的面积比即可.
④:特称命题“?x∈[1,2],x
2-1≥0”的否定是:把?改为?,其它条件不变,然后否定结论,变为一个特称命题.即“?x∈[1,2],x
2-1<0”.
解答:解:对于①,已知n个散点A
i(x
i,y
i),(i=1,2,3,…,n)的线性回归方程为
=bx+a,若
a=-b,(其中
=| n |
 |
| i=1 |
xi,
=| n |
 |
| i=1 |
yi),则此回归直线必经过点(
,),这说明回归直线一定经过样本中心点,故正确.
对于②:∵幂函数f(x)=(m
2-m-1)x
1-m∴m
2-m-1=1⇒m=-1或m=2
当m=2时,幂函数f(x)=(m
2-m-1)x
1-m=x
-1,
它不在R上是减函数,故错;
③:易得f′(x)=ax
2-2bx+a,
对于函数
f(x)=ax3-bx2+ax+π在R上有两个相异极值点的充要条件:
是a≠0且其导函数的判别式大于0,即a≠0且4b
2-4a
2>0,
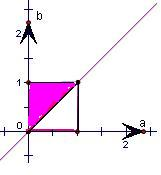
又若a,b在区间[0,1]上取值,则b>a,
点(a,b)满足的区域如图中阴影部分所示,
其中正方形区域的面积为1,阴影部分的面积为
,
但反之不能成立,因为当a,b在区间[1,2]上取值时,也得到有两相异极值点的概率为
”.故错.
对于④,全称命题“?x∈[1,2],x
2-1≥0”的否定是特称命题:“?x∈[1,2],x
2-1<0”.故正确.
故选C.
点评:本小题主要考查函数单调性的应用、命题的否定、线性回归方程、几何概型等基础知识,考查运算求解能力,考查转化思想.属于基础题.






 ③:易得f′(x)=ax2-2bx+a,
③:易得f′(x)=ax2-2bx+a,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案