
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性并求当
的奇偶性并求当![]() 时函数
时函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]() 在
在![]() 范围内有实数解,求实数
范围内有实数解,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试,若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.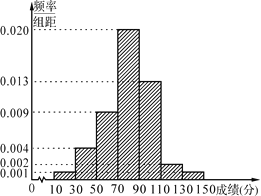
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为![]() 元,低于
元,低于![]() 箱按原价销售,不低于
箱按原价销售,不低于![]() 箱则有以下两种优惠方案:①以
箱则有以下两种优惠方案:①以![]() 箱为基准,每多
箱为基准,每多![]() 箱送
箱送![]() 箱;②通过双方议价,买方能以优惠
箱;②通过双方议价,买方能以优惠![]() 成交的概率为
成交的概率为![]() ,以优惠
,以优惠![]() 成交的概率为
成交的概率为![]() .
.
![]() 甲、乙两单位都要在该厂购买
甲、乙两单位都要在该厂购买![]() 箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
![]() 某单位需要这种零件
某单位需要这种零件![]() 箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
A.方程①有实根或方程②无实根B.方程①有实根或方程②有实根
C.方程①无实根或方程②无实根D.方程①无实根或方程②有实根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com