
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴端点和焦点所组成的四边形为正方形,且椭圆
的短轴端点和焦点所组成的四边形为正方形,且椭圆![]() 上任意一点到两个焦点的距离之和为
上任意一点到两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
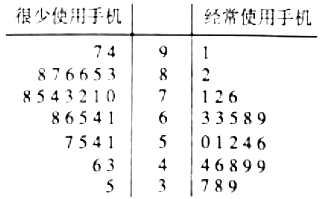
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 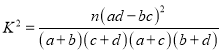 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD的顶点P在底面ABCD上的投影恰好是A,其正视图与侧视图都是腰长为a的等腰直角三角形.则在四棱锥P﹣ABCD的任意两个顶点的连线中,互相垂直的异面直线共有 对.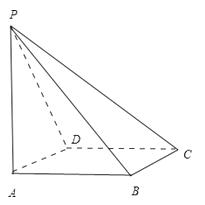
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|﹣1.
(1)证明函数f(x)是偶函数;
(2)在如图所示的平面直角坐标系中作出函数f(x)的图象.并根据图象写出函数f(x)的单调区间; 
(3)求函数f(x)当x∈[﹣2,4]时的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若f(1)= ![]() ,试求f(x)在区间[﹣2,6]上的最值.
,试求f(x)在区间[﹣2,6]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,1为函数
的极值点,1为函数![]() 的一个零点,求函数
的一个零点,求函数![]() 在
在![]() 上的最小值.
上的最小值.
(2)当![]() 时,函数
时,函数![]() 与
与![]() 轴在
轴在![]() 内有两个不同的交点,求
内有两个不同的交点,求![]() 的取值范围.(其中
的取值范围.(其中![]() 是自然对数的底数)
是自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com