
【题目】已知p:方程 ![]() =1表示焦点在x轴上的椭圆,q:双曲线
=1表示焦点在x轴上的椭圆,q:双曲线 ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ).
).
(1)若椭圆 ![]() =1的焦点和双曲线
=1的焦点和双曲线 ![]() =1的顶点重合,求实数m的值;
=1的顶点重合,求实数m的值;
(2)若“p∧q”是真命题,求实数m的取值范围.
【答案】
(1)解:由双曲线 ![]() =1,得m>0,且a2=5,a=
=1,得m>0,且a2=5,a= ![]() .
.
∵椭圆 ![]() =1的焦点和双曲线
=1的焦点和双曲线 ![]() =1的顶点重合,
=1的顶点重合,
∴椭圆 ![]() =1的焦点在x轴上,且a2=9﹣m,b2=2m,则
=1的焦点在x轴上,且a2=9﹣m,b2=2m,则 ![]() ,
,
∴ ![]() ,解得m=
,解得m= ![]()
(2)解:∵方程 ![]() =1表示焦点在x轴上的椭圆,
=1表示焦点在x轴上的椭圆,
∴9﹣m>2m>0,即0<m<3,
∵双曲线 ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ),
),
∴ ![]() (
( ![]() ),即
),即 ![]() ,
,
若“p∧q”是真命题,则 ![]() <m<3
<m<3
【解析】(1)由双曲线方程可知双曲线的焦点在x轴上,进一步可得椭圆的焦点在x轴上,求出椭圆的半焦距与双曲线的实半轴长,列等式求得m值;(2)由方程 ![]() =1表示焦点在x轴上的椭圆,双曲线
=1表示焦点在x轴上的椭圆,双曲线 ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() )分别求出m的范围,结合“p∧q”是真命题,取交集得答案.
)分别求出m的范围,结合“p∧q”是真命题,取交集得答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】国家实施二孩放开政策后,为了了解人们对此政策持支持态度是否与年龄有关,计生部门将已婚且育有一孩的居民分成中老年组(45岁以上,含45岁)和中青年组(45岁以下,不含45岁)两个组别,每组各随机调查了50人,对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图,如图所示: 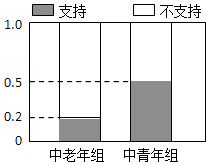
支持 | 不支持 | 合计 | |
中老年组 | 50 | ||
中青年组 | 50 | ||
合 计 | 100 |
(1)根据以上信息完成2×2列联表;
(2)是否有99%以上的把握认为人们对此政策持支持态度与年龄有关?
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0),过其焦点F的直线l交抛物线C于点A、B,|AF|=3|BF|,则|AB|=( )
A.p
B.![]()
C.2p
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组抽出的号码为28,则第8组抽出的号码应是a;若用分层抽样方法,则50岁以下年龄段应抽取b人,那么a+b等于( ) 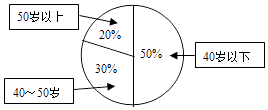
A.46
B.45
C.70
D.69
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() 、
、 ![]() 满足|
满足| ![]() |=1,|
|=1,| ![]() |=2,
|=2, ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
(1)若(k ![]() ﹣
﹣ ![]() )⊥(
)⊥( ![]() +
+ ![]() ),求k的值;
),求k的值;
(2)若|k ![]() ﹣
﹣ ![]() |<2,求k的取值范围.
|<2,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com