Question

已知集合A={x|x²-3x+2=0}，B={x|x²-mx+m-1=0}，若B⊆A，求实数m的取值范围．

Answer 1

解：化简条件得A={1，2}，
由于B⊆A，
根据集合中元素个数，集合B分类讨论，B=∅，B={1}或{2}，B={1，2}
当B=∅时，△=m²-4（m-1）＜0
∴m无解，
当B={1}或{2}时，，
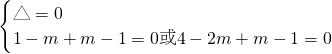
∴m=2
当B={1，2}时，
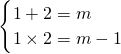
∴m=3．
综上所述，m=3或2．
分析：由题设得A={1，2}，根据B⊆A，根据集合中元素个数集合B分类讨论，B=∅，B={1}或{2}，B={1，2}，由此求解实数m的取值范围．
点评：本题考查集合的交集及其运算的应用，综合性强，具有一定的难度．解题时要认真审题，仔细解答，注意分类讨论思想的合理运用．