
 f(-1+2)=
f(-1+2)= f(1)=-
f(1)=- ,
, ×(
×(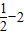 )=-
)=-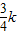 ;
; x(x+2)
x(x+2)
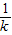 ,f(1)=-1.
,f(1)=-1. >-1,即k>1时,f(x)在x=1处取得最小值-1,
>-1,即k>1时,f(x)在x=1处取得最小值-1,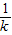 =-1,即k=1时,f(x)在x=±1处都取得最小值-1.
=-1,即k=1时,f(x)在x=±1处都取得最小值-1.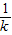 <-1,即0<k<1时,f(x)在x=-1处取得最小值-
<-1,即0<k<1时,f(x)在x=-1处取得最小值- .
.

科目:高中数学 来源: 题型:
| A、0 | B、2011 | C、4022 | D、8044 |
查看答案和解析>>
科目:高中数学 来源:江西省重点中学协作体2012届高三第一次联考数学文科试题 题型:013
设f(x),g(x),h(x)是R上的任意实值函数,如下定义两个函数(f·g)x和(f·g)(x):对任意x∈R,(f·g)(x)=f(g(x));(f·g)(x)=f(x)g(x),则下列等式恒成立的是
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)■(选项一样)
查看答案和解析>>
科目:高中数学 来源:江西省重点中学协作体2012届高三第一次联考数学理科试题 题型:013
设f(x),g(x),h(x)是R上的实值函数,如下定义两个函数(f·g)(x)和(f·g)(x):对任意x∈R,(f·g)(x)=f(g(x));(f·g)(x)=f(x)g(x),则下列等式恒成立的是
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)
((f·g)·h)(x)=((f·h)·(g·h))(x)
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第05课时):第一章 集合与简易逻辑-简易逻辑(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com