
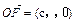 (c>0),
(c>0),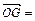 (n, n)(n∈R),
(n, n)(n∈R), 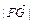 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①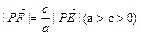 ,②
,②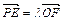 (其中
(其中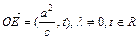 );③动点P的轨迹C经过点B(0,-1)。
);③动点P的轨迹C经过点B(0,-1)。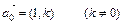 的直线l与曲线C交于不同两点M、N,若
的直线l与曲线C交于不同两点M、N,若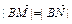 ,求k的取值范围。
,求k的取值范围。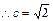
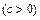 ,(2)曲线C的方程为:
,(2)曲线C的方程为: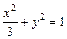 ,
,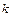 的取值范围是
的取值范围是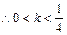 。
。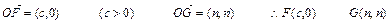
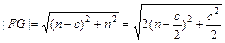
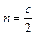 时,
时,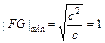
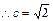
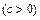
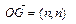 可知点G在直线y=x上
可知点G在直线y=x上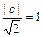
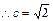 (
(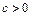 )
)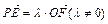 知
知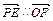 又
又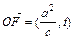
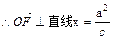
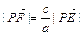 (
( )∴
)∴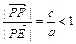 ∴点P在以F为焦点,
∴点P在以F为焦点,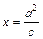 为准线的椭圆上
为准线的椭圆上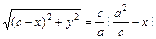 ∵动点P的轨迹C经过点B(0,-1)且
∵动点P的轨迹C经过点B(0,-1)且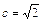
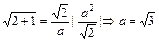 从而b="1 " ∴曲线C的方程为:
从而b="1 " ∴曲线C的方程为: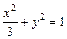
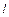 的方程为
的方程为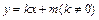
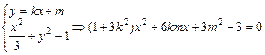
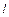 与曲线C交于不同两点,∴
与曲线C交于不同两点,∴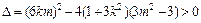 ,即
,即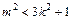 ①
①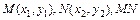 的中点
的中点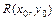 由
由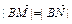 则有BR⊥MN
则有BR⊥MN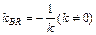 (11分)由韦达定理有
(11分)由韦达定理有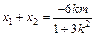
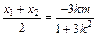 ∴MN的中点R0坐标为
∴MN的中点R0坐标为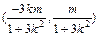 (12分)又B(0,-1)
(12分)又B(0,-1)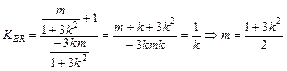 ②
②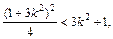
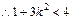
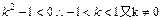 ∴
∴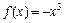 为R上的减函数
为R上的减函数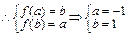 (3分)志求闭区间为[-1,1]
(3分)志求闭区间为[-1,1]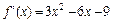 (5分)(或∵
(5分)(或∵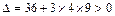 )∴
)∴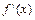 在R不可能恒为正式恒为负)
在R不可能恒为正式恒为负)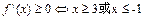
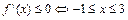
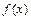 在R上不是单调函数,故
在R上不是单调函数,故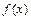 不是闭函数
不是闭函数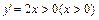
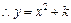 在(0,
在(0,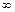 )上是增函数
)上是增函数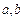 ]
]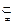 (0,∞),
(0,∞),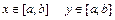
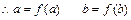
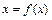 有两个不相等的正根
有两个不相等的正根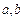 (12分)
(12分)
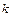 的取值范围是
的取值范围是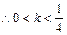


科目:高中数学 来源:不详 题型:解答题
 轴,
轴,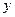 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且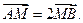
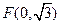 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线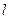 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段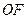 上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
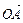 (
( cos
cos ,
,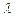 sin
sin ) (
) ( ≠0 ),
≠0 ),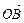 =" (" – sin
=" (" – sin ,cos
,cos ),其中O为坐标原点。(1)若
),其中O为坐标原点。(1)若 =
= –
– 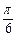 ,求向量
,求向量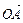 与
与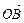 的夹角;(2)若|
的夹角;(2)若|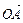 |≥2|
|≥2|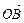 |对任意实数
|对任意实数 、
、 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
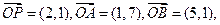 设
设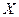 是直线
是直线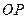 上的一点, (其中
上的一点, (其中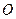 为坐标原点).
为坐标原点).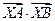 取最小值时的点
取最小值时的点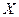 的坐标和此时
的坐标和此时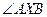 的余弦值.
的余弦值. 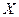 .若
.若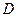 是线段
是线段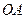 的三等分点,且
的三等分点,且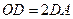 ,
,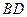 与
与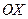 交于点
交于点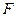 ,设
,设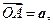
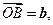 试用
试用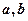 表示
表示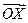 和
和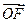 .
. 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com