
(12分) 甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为 ,乙投篮命中的概率为
,乙投篮命中的概率为 .
.
(1)求甲至多命中2个且乙至少命中2个的概率;
(2)若规定每投篮一次命中得3分,未命中得 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 | 射手乙 | ||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 |
| 概率 |  |  |  | 概率 |  | 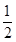 |  |
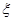 ,求
,求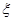 的分布列和期望.
的分布列和期望. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为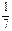 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取, ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
(1)则袋中原有白球的个数;
(2)取球2次终止的概率;
(3)甲取到白球的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
车站每天8∶00~9∶00,9∶00~10∶00都恰有一辆客车到站,8∶00~9∶00到站的客车A可能在8∶10,8∶30,8∶50到站,其概率依次为 ;9∶00~10∶00到站的客车B可能在9∶10,9∶30,
;9∶00~10∶00到站的客车B可能在9∶10,9∶30, 9∶50到站,其概率依次为
9∶50到站,其概率依次为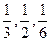 .
.
(1)旅客甲8∶00到站,设他的候车时间为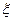 ,求
,求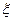 的分布列和
的分布列和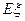 ;
;
(2)旅客乙8∶20到站,设他的候车时间为 ,求
,求 的分布列和
的分布列和 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)
检测部门决定对某市学校教室的 空气质量进行检测,空气质量分为A、B、C三级.
空气质量进行检测,空气质量分为A、B、C三级.
每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为 ,
, ,
, .
.
(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为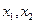 ,记
,记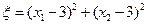 .
.
(1)分别求出 取得最大值和最小值时的概率; (2)
取得最大值和最小值时的概率; (2) 求
求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com