
分析 依次令n=1、2、3、4…,分别计算f(1)、f(2)、f(3)、f(4)…,根据规律归纳f(x)的解析式即可计算出答案.
解答 解:令n=1得f(f(1))=3,
若f(1)=1,则f(f(1))=f(1)=1,与f(f(1))=3矛盾;
若f(1)=3,则f(f(1))=f(3)=3,与f(x)是增函数矛盾;
同理f(1)不可能大于3,
∴f(1)=2,
∴f(f(1))=f(2)=3,
令n=2得f(f(2))=f(3)=6,
令n=3得f(f(3))=f(6)=9,
∴f(4)=7,f(5)=8.
令n=4得f(f(4))=f(7)=12,
令n=5得f(f(5))=f(8)=15,
令n=6得f(f(6))=f(9)=18,
令n=7得f(f(7))=f(12)=21,
∴f(10)=19,f(11)=20,
令n=8得f(f(8))=f(15)=24,
∴f(13)=22,f(14)=22
…
归纳可得:当n≥9时,f(n)=n+9,
∴f(2017)-f(1999)=(2017+9)-(1999+9)=18.
故答案为18.
点评 本题考查了抽象函数的函数值计算,归纳推理,属于中档题.


科目:高中数学 来源: 题型:选择题
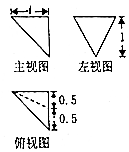
| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{27-n}^{8}$ | B. | A${\;}_{34-n}^{27-n}$ | C. | A${\;}_{34-n}^{7}$ | D. | A${\;}_{34-n}^{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.
在平面直角坐标系中,已知两定点$A(-\frac{1}{3}\;,\;0)$和$B({\frac{1}{3}\;,\;0})$,点M是平面内的动点,且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com