
分析 ( I)求出函数f(x)、g(x)的定义域,再根据交集的定义写出A∩B;
( II)根据补集与交集的定义,结合一元二次不等式与方程的知识,即可求出a的值.
解答 解:( I)函数$f(x)=\sqrt{5-x}+lg(x+1)$有意义,
则有$\left\{\begin{array}{l}5-x≥0\\ x+1>0\end{array}\right.$,
解得-1<x≤5,-----------(2分)
当a=-8时,g(x)=lg(x2-2x-8),
所以x2-2x-8>0,
解得x>4或x<-2,-----------(4分)
所以A∩B={x|4<x≤5};------------(5分)
(II)∁RB={x|x2-2x+a≤0}={x|x1≤x≤x2},--------------(6分)
由A∩(∁RB)={x|-1<x≤3},
可得x1≤-1,x2=3,-------------(8分)
将x2=3带入方程,解得a=-3,x1=-1,满足题意,
所以a=-3.--------------(10分)
点评 本题考查了集合的定义与运算问题,也考查了一元二次不等式与方程的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,-1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B是必然事件 | B. | C∪D是必然事件 | C. | C与D一定互斥 | D. | C与D一定不互斥 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
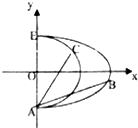 已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲线C2:x2+y2=r2(x≥0)都过点A(0,-1),且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$
已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲线C2:x2+y2=r2(x≥0)都过点A(0,-1),且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com