练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，AB＝PA＝1，AD，F是PB中点，E为BC上一点.

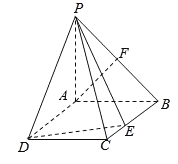
    （1）求证：AF⊥平面PBC；

    （2）当BE为何值时，二面角C﹣PE﹣D为45°.

    【答案】（1）证明见解析（2）BE

    【解析】

    （1）以为原点，为轴，为轴，为轴，建立空间直角坐标系，利用向量法能证明平面．

    （2）设，，求出平面的法向量和平面的法向量，利用向量法能求出当时，二面角为．

    解：（1）证明：以为原点，为轴，为轴，为轴，建立空间直角坐标系，

    ，，是中点，

    ，0，，，0，，，1，，，1，，，

    ，，，，，

    ，，，

    ，，

    ，，

    平面．

    （2）设，，1，，，，

    设平面的法向量，

    则，

    取，得，，，

    平面的法向量为，

    二面角为，

    ，

    解得，

    当时，二面角为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在五面体中，侧面是正方形，是等腰直角三角形，点是正方形对角线的交点，且.

    （1）证明：平面；

    （2）若侧面与底面垂直，求五面体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC-A1B1C1中，点M，N分别为线段A1B，B1C的中点．

    （1）求证：MN∥平面AA1C1C；

    （2）若∠ABC=90°，AB=BC=2，AA1=3，求点B1到面A1BC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地随着经济的发展，居民收入逐年增长该地一建设银行统计连续五年的储蓄存款（年底余额）得到下表：

    年份x

    2014

    2015

    2016

    2017

    2018

    储蓄存款y（千亿元）

    5

    6

    7

    8

    10

    为便于计算，工作人员将上表的数据进行了处理（令），得到下表：

    时间t

    1

    2

    3

    4

    5

    储蓄存款z

    0

    1

    2

    3

    5

    （1）求z关于t的线性回归方程；

    （2）通过（1）中的方程，求出y关于x的回归方程；

    （3）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？

    附：线性回归方程，其中，.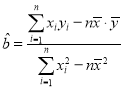

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2＋y2＋2x－4y＋3＝0．

    (1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程．

    (2)从圆C外一点P(x1，y1)向该圆引一条切线，切点为M，O为坐标原点，且有|PM|＝|PO|，求使得|PM|取得最小值的点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，求函数的单调减区间；

    （2）若关于x的不等式恒成立，求实数a的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某年级100名学生期中考试数学成绩（单位:分）的频率分布直方图如图所示，其中成绩分组区间是[50，60)，[60，70)，[70，80)，[80，90)，[90，100].

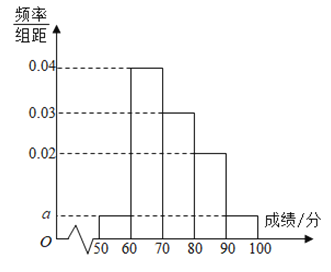
    （1）求图中a的值，并根据频率分布直方图估计这100名学生数学成绩的平均分；

    （2）从[70，80)和[80，90)分数段内采用分层抽样的方法抽取5名学生，求在这两个分数段各抽取的人数；

    （3）现从第（2）问中抽取的5名同学中任选2名参加某项公益活动，求选出的两名同学均来自[70，80)分数段内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点及圆.

    (1)若直线过点且与圆心的距离为1，求直线的方程；

    (2)设过点的直线与圆交于两点，当时，求以线段为直径的圆的方程；

    (3)设直线与圆交于两点，是否存在实数，使得过点的直线垂直平分弦？若存在，求出实数的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在（0，+∞）上的增函数，且满足f（xy）=f（x）+f（y），f（2）=1．

    （1）求f（8）的值；

    （2）求不等式f（x）-f（x-2）＞3的解集．

    查看答案和解析>>

    同步练习册答案