
【题目】数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,证明
,证明![]() 是等差数列;
是等差数列;
(2)求![]() 的通项公式.
的通项公式.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即可证得;
(2)由(1)得bn=1+2(n-1)=2n-1,即an+1-an=2n-1,进而利用累加求通项公式即可.
试题解析:
(1)证明 由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即bn+1=bn+2.
又b1=a2-a1=1,所以{bn}是首项为1,公差为2的等差数列.
(2)解 由(1)得bn=1+2(n-1)=2n-1,即an+1-an=2n-1.
于是![]() (ak+1-ak)=
(ak+1-ak)=![]() (2k-1),所以an+1-a1=n2,即an+1=n2+a1.
(2k-1),所以an+1-a1=n2,即an+1=n2+a1.
又a1=1,所以an=n2-2n+2,经检验,此式对n=1亦成立,
所以,{an}的通项公式为an=n2-2n+2.


科目:高中数学 来源: 题型:
【题目】在一个试验中,把一种血清注射到500只豚鼠体内,被注射前,这些豚鼠中150只有圆形细胞,250只有椭圆形细胞,100只有不规则形状细胞;被注射后,没有一个具有圆形细胞的豚鼠被感染,50个具有椭圆形细胞的豚鼠被感染,具有不规则形状细胞的豚鼠全部被感染,根据试验结果,估计具有下列类型的细胞的豚鼠被这种血清感染的概率;
(1)圆形细胞;
(2)椭圆形细胞;
(3)不规则形状细胞.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点落在半径为
的三个顶点落在半径为![]() 的球
的球![]() 的表面上,三角形有一个角为
的表面上,三角形有一个角为![]() 且其对边长为3,球心
且其对边长为3,球心![]() 到
到![]() 所在的平面的距离恰好等于半径
所在的平面的距离恰好等于半径![]() 的一半,点
的一半,点![]() 为球面上任意一点,则
为球面上任意一点,则![]() 三棱锥的体积的最大值为( )
三棱锥的体积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水域受到污染,水务部门决定往水中投放一种药剂来净化水质,已知每次投放质量为![]() 的药剂后,经过
的药剂后,经过![]() (
(![]() )天,该药剂在水中释放的浓度
)天,该药剂在水中释放的浓度![]() (毫克
(毫克![]() 升)为
升)为![]() ,其中
,其中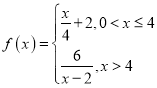 ,当药剂在水中释放浓度不低于
,当药剂在水中释放浓度不低于![]() (毫克
(毫克![]() 升)时称为有效净化,当药剂在水中释放的浓度不低于
升)时称为有效净化,当药剂在水中释放的浓度不低于![]() (毫克
(毫克![]() 升)且不高于
升)且不高于![]() (毫克
(毫克![]() 升)时称为最佳净化.
升)时称为最佳净化.
(1)如果投放的药剂质量为![]() ,那么该水域达到有效净化一共可持续几天?
,那么该水域达到有效净化一共可持续几天?
(2)如果投放的药剂质量为![]() ,为了使该水域
,为了使该水域![]() 天(从投放药剂算起,包括第
天(从投放药剂算起,包括第![]() 天)之内都达到最佳净化,确定应该投放的药剂质量
天)之内都达到最佳净化,确定应该投放的药剂质量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.
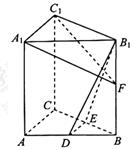
求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.

若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在点![]() 发现乙船在北偏东
发现乙船在北偏东![]() 的
的![]() 处,
处,![]() 里,且乙船以每小时10里的速度向正北行驶,已知甲船的速度是每小时
里,且乙船以每小时10里的速度向正北行驶,已知甲船的速度是每小时![]() 里,问:甲船以什么方向前进,才能与乙船最快相遇,相遇时甲船行驶了多少小时?
里,问:甲船以什么方向前进,才能与乙船最快相遇,相遇时甲船行驶了多少小时?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com