
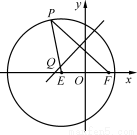
如图,已知圆E 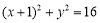 ,点
,点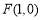 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹 的方程;
的方程;
(2)点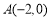 ,
,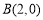 ,点G是轨迹
,点G是轨迹 上的一个动点,直线AG与直线
上的一个动点,直线AG与直线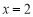 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
(1)点Q的轨迹 的方程为为
的方程为为 .(2)以线段BD为直径的圆与直线GF相切.
.(2)以线段BD为直径的圆与直线GF相切.
【解析】
试题分析:(1)连结QF,由于线段的垂直平分线上的点到线段两端点的距离相等,所以|QE|+|QF|=|QE|+|QP|=4 ,根据椭圆的定义知,动点Q的轨迹
,根据椭圆的定义知,动点Q的轨迹 是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为
是以E,F为焦点,长轴长为4的椭圆.由此便可得其方程;(2)直线与圆的位置关系一般通过比较圆心到直线的距离与圆的半径的大小关系来确定. 由题意,设直线AG的方程为 ,则点D坐标为
,则点D坐标为 ,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为
,由此可得圆心和半径.下面用k表示点G的坐标,求出直线GF方程为 ,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.
,进而求到圆心到直线GF的距离便可知道以BD为直径的圆与直线GF的位置关系.
(1)连结QF,根据题意,|QP|=|QF|,
则|QE|+|QF|=|QE|+|QP|=4 ,
,
故Q的轨迹 是以E,F为焦点,长轴长为4的椭圆. .2分
是以E,F为焦点,长轴长为4的椭圆. .2分
设其方程为 ,可知
,可知 ,
, ,则
,则 , ..3分
, ..3分
所以点Q的轨迹 的方程为为
的方程为为 . 4分
. 4分
(2)以线段BD为直径的圆与直线GF相切. 5分

由题意,设直线AG的方程为 ,则点D坐标为
,则点D坐标为 ,BD的中点H的坐标为
,BD的中点H的坐标为 .
.
联立方程组 消去y得
消去y得 ,
,
设 ,则
,则 ,
,
所以 ,
, , 7分
, 7分
当 时,点G的坐标为
时,点G的坐标为 ,点D的坐标为
,点D的坐标为 .
.
直线GF⊥x轴,此时以BD为直径的圆 与直线GF相切. 9分
与直线GF相切. 9分
当 时,则直线GF的斜率为
时,则直线GF的斜率为 ,则直线GF方程为
,则直线GF方程为 ,
,
点H到直线GF的距离 ,又
,又 ,
,
所以圆心H到直线GF的距离 ,此时,以BD为直径的圆与直线GF相切.
,此时,以BD为直径的圆与直线GF相切.
综上所述,以线段BD为直径的圆与直线GF相切. 13分
考点:1、椭圆的方程;2、直线与椭圆的关系;3、最值问题.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
设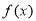 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当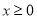 时,
时,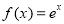 。若对任意的x
。若对任意的x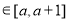 ,不等式
,不等式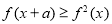 恒成立,则实数a的最大值是( )。
恒成立,则实数a的最大值是( )。
(A)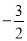 (B)
(B)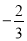 (C)
(C)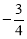 (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入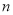 的值为3,则输出
的值为3,则输出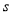 的值是( )
的值是( )

A.1 B.2 C.4 D.7
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试理科数学试卷(解析版) 题型:选择题
在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成如图所示的人体脂肪含量与年龄关系的散点图.根据该图,下列结论中正确的是( )

(A)人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20%
(B)人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20%
(C)人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20%
(D)人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20%
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:填空题
设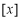 表示不超过
表示不超过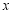 的最大整数,如:
的最大整数,如: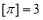 ,
,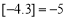 .给出下列命题:
.给出下列命题:
①对任意实数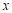 ,都有
,都有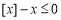 ;
;
②若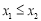 ,则
,则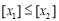 ;
;
③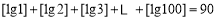 ;
;
④若函数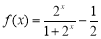 ,则
,则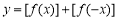 的值域为
的值域为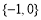 .
.
其中所有真命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省资阳市高三下学期4月高考模拟考试文科数学试卷(解析版) 题型:选择题
已知实数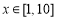 ,执行右图所示的程序框图,则输出x的值不小于55的概率为( )
,执行右图所示的程序框图,则输出x的值不小于55的概率为( )
(A)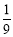 (B)
(B)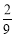 (C)
(C)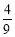 (D)
(D)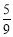
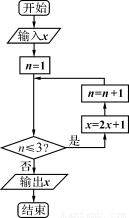
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三第六期3月阶段性考试文科数学试卷(解析版) 题型:填空题
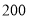 辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速在
辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速在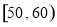 的汽车大约有______辆.
的汽车大约有______辆.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com