
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
| 2 |
| 2+1 |
| 22 |
| 22+1 |
| 2n |
| 2n+1 |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
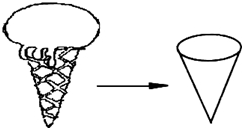 如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.| h |
| r |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 用电量(千瓦时) | 电费(元|千瓦时) |
| 不超过200的部分 | 0.56 |
| 超过200至300的部分 | 0.64 |
| 超过300的部分 | 0.96 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 10000 |
| x |
| A、1150万元 |
| B、1000万元 |
| C、950万元 |
| D、900万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com