
【题目】已知![]() (
(![]() ,
,![]() 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数![]() 在
在![]() 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间![]() ,使函数
,使函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,那么称
,那么称![]() ,
,![]() 为闭函数;
为闭函数;
请解答以下问题:
(1) 求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2) 判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围;
的取值范围;
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,总存在实数
,总存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 关于参数
关于参数![]() 的不动点.
的不动点.
(1)当![]() ,
,![]() 时,求
时,求![]() 关于参数
关于参数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有关于参数
恒有关于参数![]() 两个不动点,求
两个不动点,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 上存在两个关于参数
上存在两个关于参数![]() 的不动点,试求参数
的不动点,试求参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是![]() ,现采用随机模拟的方法估计该运动员射击
,现采用随机模拟的方法估计该运动员射击![]() 次至多击中
次至多击中![]() 次的概率:先由计算器产生
次的概率:先由计算器产生![]() 到
到![]() 之间取整数值的随机数,指定
之间取整数值的随机数,指定![]() 、
、![]() 表示没有击中目标,
表示没有击中目标,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示击中目标,因为射击
表示击中目标,因为射击![]() 次,故以每
次,故以每![]() 个随机数为一组,代表射击
个随机数为一组,代表射击![]() 次的结果.经随机模拟产生了如下
次的结果.经随机模拟产生了如下![]() 组随机数:
组随机数:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
据此估计,射击运动员射击4次至多击中3次的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: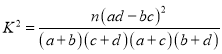 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱中![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
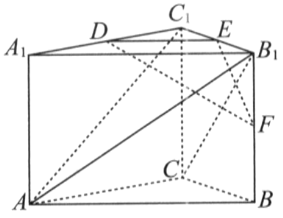
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?如果存在,求出线段
?如果存在,求出线段![]() 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W:![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)判断点A与以CD为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划在甲、乙两个互联网创新项目上共投资1200万元,每个项目至少要投资300万元.根据市场分析预测:甲项目的收益![]() 与投入
与投入![]() 满足
满足![]() ,乙项目的收益
,乙项目的收益![]() 与投入
与投入![]() 满足
满足![]() .设甲项目的投入为
.设甲项目的投入为![]() .
.
(1)求两个项目的总收益关于![]() 的函数
的函数![]() .
.
(2)如何安排甲、乙两个项目的投资,才能使总收益最大?最大总收益为多少?(注:收益与投入的单位都为“万元”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com