
已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数 与时刻
与时刻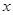 (时)的关系为
(时)的关系为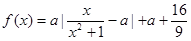 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且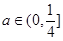 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作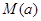 .
.
(1)令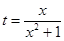 ,
, ,求
,求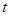 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果n件产品中任取一件样品是次品的概率为 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
).
(1)求该企业日赢利额 的最大值;
的最大值;
(2)为保证每天的赢利额不少于日赢利额最大值的50%,试求该企业日产量的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
请你设计一个包装盒,如图所示, 是边长为
是边长为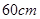 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.
(1)若广告商要求包装盒侧面积 最大,试问
最大,试问 应取何值?
应取何值?
(2)若广告商要求包装盒容积 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为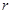 米,高为
米,高为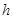 米,体积为
米,体积为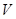 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为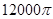 元(
元(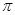 为圆周率).
为圆周率).
(1)将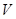 表示成
表示成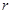 的函数
的函数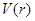 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数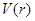 的单调性,并确定
的单调性,并确定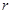 和
和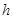 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•湖北)(1)已知函数f(x)=lnx﹣x+1,x∈(0,+∞),求函数f(x)的最大值;
(2)设a1,b1(k=1,2…,n)均为正数,证明:
①若a1b1+a2b2+…anbn≤b1+b2+…bn,则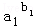
 …
…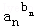 ≤1;
≤1;
②若b1+b2+…bn=1,则 ≤
≤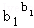
 …
…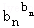 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com