
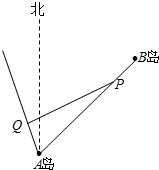
 已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.
已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.分析 (1)设航行时间为t,利用余弦定理求出PQ的表达式,求出最小值.
(2)小船P处于小船Q的正东方向时,∠APQ=45°,利用正弦定理求出AQ,
解答 解:(1)设航行时间为t,(0≤t≤5),则AP=10-2t,AQ=4t,∠PAQ=45°+15°=60°,
∴PQ2=(10-2t)2+(4t)2-2(10-2t)•4tcos60°=28t2-80t+100,
∴PQ2的最小值是$\frac{4×28×100-8{0}^{2}}{4×28}$=$\frac{300}{7}$.∴PQ的最小距离是$\frac{10\sqrt{21}}{7}$.
(2)当小船P处于小船Q的正东方向时,∠APQ=45°,∠AQP=75°,由正弦定理得:$\frac{AQ}{sin∠APQ}=\frac{AP}{sin∠AQP}$,
∴$\frac{4t}{sin45°}=\frac{10-2t}{sin75°}$,解得t=10-5$\sqrt{3}$.∴当小船P处于小船Q的正东方向时,小船航行的时间为10-5$\sqrt{3}$小时.
点评 本题考查了利用正余弦定理解三角形的实际应用,是中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
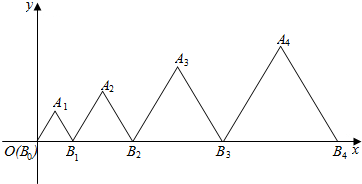 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
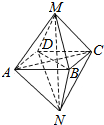 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )| A. | 该几何体是由两个同底的四棱锥组成的几何体 | |
| B. | 该几何体有12条棱、6个顶点 | |
| C. | 该几何体有8个面,并且各面均为三角形 | |
| D. | 该几何体有9个面,其中一个面是四边形,其余均为三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 1个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com