【题目】已知函数
.
（1）判断方程
的根个数；
（2）若
时，
恒成立，求实数
的取值范围.
【答案】（1）
；
【解析】
（1）首先设
，求导得到
，求出函数
的单调区间，根据单调区间得到
，又因为
时，
，
，从而得到方程
有两个根.
（2）首先设
，将题意转化为
，
恒成立.再讨论
的范围，利用导数得到函数
的单调性，确定
，由
即可得到实数的取值范围.
（1）设
，
.
.
因为，所以
.
令
，解得
.
当
，
，为减函数，
当
，
，为增函数.
所以
.
又因为时，，，
所以函数与
轴有个交点，即方程有2个根.
（2）设
将题意等价于，恒成立.
，
因为，所以
.
当
，即
时，
.
令
，解得
.
，
，为减函数，
，
，为增函数.
，不满足恒成立，舍去.
当
，即
时，令，解得或
.
①当
时，
，
，在
为增函数，
，不满足恒成立，舍去.
②当
时，即
.
，，为增函数，
，，为减函数，
，，为增函数，
又因为
，
，
所以
，不满足恒成立，舍去.
③当
时，即
.
，，为增函数，
，，为减函数，
，，为增函数，
又因为
，
，
因为时，恒成立，
所以
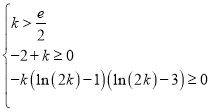，解得
.
综上所述：实数的取值范围为.
科目：高中数学 来源： 题型：
【题目】已知椭圆
的右焦点为
，右准线为
.点
是椭圆
上异于长轴端点的任意一点，连接
并延长交椭圆于点
，线段
的中点为
，
为坐标原点，且直线
与右准线
交于点
.
（1）求椭圆的标准方程；
（2）若
，求点的坐标；
（3）试确定直线
与椭圆的公共点的个数，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为改善环境，节约资源，我国自2019年起在全国地级及以上城市全面启动生活垃圾分类，垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关，对该小区居民进行了随机抽样调查，得到如下统计数据的列联表：
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
（1）求列联表中的
，
，
，
，
的值，并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率；
（2）根据列联表判断能否有
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关？
参考数据及公式：
|
|
|
|
|
|
|
|
|
|
|
|
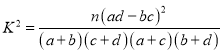，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1,AB=2,AB∥DC，∠BCD=900
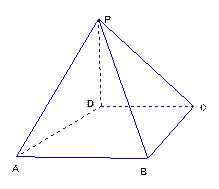
（1）求证：PC⊥BC
（2）求点A到平面PBC的距离
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在锐角△ABC中，a＝2
，_______，求△ABC的周长l的范围．
在①
(﹣cos
，sin)，
(cos，sin)，且
，②cosA(2b﹣c)＝acosC，③f(x)＝cosxcos(x
)
，f(A)
注：这三个条件中任选一个，补充在上面问题中并对其进行求解．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
