
【题目】如图所示,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,F是PB的中点.求证:
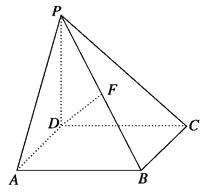
(1)DF⊥AP.
(2)在线段AD上是否存在点G,使GF⊥平面PBC?若存在,说明G点的位置,并证明你的结论;若不存在,说明理由.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)取AB的中点E,连结EF,则PA∥EF.由题意可得DE2=EF2+DF2,从而DF⊥EF,结合EF∥PA,可证得DF⊥PA.(2)猜想当G点是AD的中点,满足GF⊥平面PBC。连PG、BG,可得GF⊥PB,又由条件可得GF⊥BC,从而可证得GF⊥平面PBC,从而得到假设成立。
试题解析:
(1)取AB的中点E,连结EF,则PA∥EF.
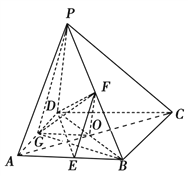
设PD=DC=a,
易求得DE=![]() a,FE=
a,FE=![]() PA=
PA=![]() a,DF=
a,DF=![]() PB=
PB=![]() a.
a.
由于DE2=EF2+DF2,
故DF⊥EF,
又EF∥PA,
∴DF⊥PA.
(2)在线段AD上存在点G,使GF⊥平面PBC,且G点是AD的中点.
取AD的中点G,连接PG、BG,则PG=BG.
又F为PB的中点,故GF⊥PB.
∵F为PB中点,
∴F点在底面ABCD上的射影为正方形ABCD的中心O,
∴GO为GF在平面ABCD上的射影,
∵GO⊥BC,
∴GF⊥BC,
又BC∩PB=B,
∴GF⊥平面PBC.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D为线段AC的中点.
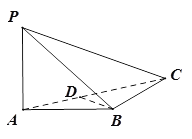
(1)求证:PA⊥BD.
(2)求证:BD⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三人独立破译同一份密码.已知三人各自破译出密码的概率分别为 ![]() ,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
,且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前55个圈中的●的个数是( )
A.10
B.9
C.8
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型: ![]() ,其中x表示经过的时间,
,其中x表示经过的时间, ![]() 表示x=0时的人口,r表示人口的平均增长率.
表示x=0时的人口,r表示人口的平均增长率.
下表是1950―1959年我国人口数据资料:

如果以各年人口增长率的平均值作为我国这一时期的人口增长率,用马尔萨斯人口增长模型建立我国这一时期的具体人口增长模型,某同学利用图形计算器进行了如下探究:
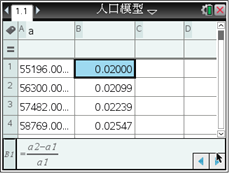
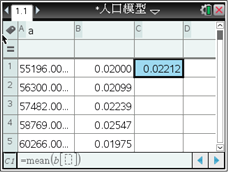
由此可得到我国1950―1959年我国这一时期的具体人口增长模型为____________. (精确到0.001)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
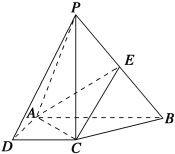
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com