
【题目】已知![]() ,满足
,满足![]() ,且
,且![]() 的两实根之积为4.
的两实根之积为4.
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() ,在
,在![]() 上的最大值(用
上的最大值(用![]() 表示).
表示).
【答案】(1)f(x)=x2-4x+4(2)g(x)max=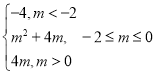
【解析】
(1)利用![]() 求得
求得![]() 的对称轴,进而求得
的对称轴,进而求得![]() ,利用根与系数关系求得
,利用根与系数关系求得![]() ,进而求得函数
,进而求得函数![]() 的解析式.
的解析式.
(2)首先化简![]() 的解析式,求得其对称轴为
的解析式,求得其对称轴为![]() ,根据对称轴和求解
,根据对称轴和求解![]() 的位置关系对
的位置关系对![]() 进行分类讨论,结合二次函数在闭区间上的值域的求法,求得
进行分类讨论,结合二次函数在闭区间上的值域的求法,求得![]() 在
在![]() 上最大值的表达式.
上最大值的表达式.
(1)根据题意,f(x)=x2+ax+b,满足f(-2)=f(6),则其对称轴x=2,
则a=-4,
又由f(x)=0的两实根之积为4,即x2+ax+b=0的两根之积为4,b=4,
则f(x)=x2-4x+4,
(2)由(1)的结论,f(x)=x2-4x+4,则g(x)=2mx-f(x)=-x2+(2m+4)x-4=-[x-(m+2)]2+m2+4m,
其对称轴为x=m+2,
分3种情况:
当m+2<0,即m<-2时,g(x)在[0,2]上为减函数,则g(x)max=g(0)=-4,
当0≤m+2≤2,即-2≤m≤0时,则g(x)max=g(m+2)=m2+4m,
当m+2>2,即m>0时,g(x)在[0,2]上为增函数,则g(x)max=g(2)=4m,
故g(x)max=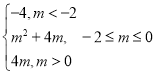 .
.


科目:高中数学 来源: 题型:
【题目】给出下列结论:
(1)某学校从编号依次为001,002,…,900的900个学生中用系统抽样的方法抽取一个样本,已知样本中有两个相邻的编号分别为053,098,则样本中最大的编号为862.
(2)甲组数据的方差为5,乙组数据为5、6、9、10、5,那么这两组数据中较稳定的是甲.
(3)若两个变量的线性相关性越强,则相关系数![]() 的值越接近于1.
的值越接近于1.
(4)对A、B、C三种个体按3:1:2的比例进行分层抽样调查,若抽取的A种个体有15个,则样本容量为30.
则正确的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]()
![]() . (其中
. (其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
(Ⅰ)证明:![]() ;
;
(Ⅱ)设![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意
对任意![]() 成立?若存在,求出
成立?若存在,求出![]() 的一个值;若不存在,请说明理由.
的一个值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
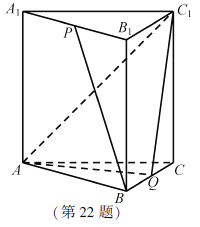
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某保险公司的推销员中随机抽取50名,统计这些推销员某月的月销售额(单位:千元),由统计结果得如图频数分别表:
月销售额 分组 | [12.25,14.75) | [14.75,17.25) | [17.25,19.75) | [19.75,22.25) | [22.25,24.75) |
频数 | 4 | 10 | 24 | 8 | 4 |

(1)作出这些数据的频率分布直方图;
(2)估计这些推销员的月销售额的平均数(同一组中的数据用该组区间的中点作代表);
(3)根据以上抽样调查数据,公司将推销员的月销售指标确定为17.875千元,试判断是否有60%的职工能够完成该销售指标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用.已知每服用m(![]() 且
且![]() )个单位的药剂,药剂在血液中的含量y(克)随着时间x(时)变化的函数关系式近似为
)个单位的药剂,药剂在血液中的含量y(克)随着时间x(时)变化的函数关系式近似为![]() ,其中
,其中 .
.
(1)若病人一次服用3个单位的药剂,则有效治疗时间可达多少小时?
(2)若病人第一次服用2个单位的药剂,4个小时后再服用m个单位的药剂,要使接下来的2个小时中能够持续有效治疗,试求m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com