
【题目】已知抛物线![]() ,
,![]() 为抛物线
为抛物线![]() 上的点,若直线
上的点,若直线![]() 经过点
经过点![]() 且斜率为
且斜率为![]() ,则称直线
,则称直线![]() 为点
为点![]() 的“特征直线”.设
的“特征直线”.设![]() 、
、![]() 为方程
为方程![]() (
(![]() )的两个实根,记
)的两个实根,记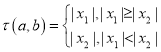 .
.
(1)求点![]() 的“特征直线”
的“特征直线”![]() 的方程;
的方程;
(2)已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 的“特征直线”与双曲线
的“特征直线”与双曲线![]() 经过二、四象限的渐进线垂直,且与
经过二、四象限的渐进线垂直,且与![]() 轴的交于点
轴的交于点![]() ,点
,点![]() 为线段
为线段![]() 上的点.求证:
上的点.求证:![]() ;
;
(3)已知![]() 、
、![]() 是抛物线
是抛物线![]() 上异于原点的两个不同的点,点
上异于原点的两个不同的点,点![]() 、
、![]() 的“特征直线”分别为
的“特征直线”分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且与
,且与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .求证:点
.求证:点![]() 在线段
在线段![]() 上的充要条件为
上的充要条件为![]() (其中
(其中![]() 为点
为点![]() 的横坐标).
的横坐标).
【答案】(1)![]() (2)证明见解析(3)证明见解析
(2)证明见解析(3)证明见解析
【解析】
(1)计算![]() 的斜率为1,再计算直线方程得到答案.
的斜率为1,再计算直线方程得到答案.
(2)根据与渐近线垂直得到![]() ,线段
,线段![]() 的方程为
的方程为![]()
![]() ,得到
,得到![]() ,代入方程得到
,代入方程得到![]() ,
,![]() ,计算得到
,计算得到![]() .
.
(3))设![]() ,
,![]() ,得到
,得到![]() 所对应的方程为:
所对应的方程为:![]() 计算得到
计算得到![]() ,分别证明充分性和必要性得到答案.
,分别证明充分性和必要性得到答案.
(1)由题意![]() 的斜率为1,所以点
的斜率为1,所以点![]() 的“特征直线”
的“特征直线”![]() 的方程为
的方程为![]() .
.
(2)设点![]() ,由于双曲线
,由于双曲线![]() 所求渐进线的斜率为
所求渐进线的斜率为![]()
所以![]() ,进而得
,进而得![]() ,线段
,线段![]() 的方程为
的方程为![]()
![]()
所以![]() 满足
满足![]()
![]()
![]() 所对应方程为:
所对应方程为:![]() ,解得
,解得![]() ,
,![]()
因为![]() ,所以
,所以![]() ,进而
,进而![]()
(3)设![]() ,
,![]() ,
,
则![]() 、
、![]() 的方程分别为
的方程分别为![]() ,
,![]() ,
,
解![]() 、
、![]() 交点可得
交点可得![]() ,
,![]() ,
,
![]() 所对应的方程为:
所对应的方程为:![]() ,
,![]()
必要性:因为点![]() 在线段
在线段![]() 上
上
当![]() 时,
时,![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ,
,
所以![]() ,进而
,进而![]()
①充分性:由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ,
,
当![]() 时,得
时,得![]() ,得
,得![]() ,
,
所以点![]() 在线段
在线段![]() 上.
上.
综上所述:点![]() 在线段
在线段![]() 上的充要条件为
上的充要条件为![]()


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,直线
,直线![]() 经过点
经过点![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.

(1)若![]() 且
且![]() ,求证:
,求证: ![]() 必为
必为![]() 的焦点;
的焦点;
(2)设![]() ,若点
,若点![]() 在
在![]() 上,且
上,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为坐标原点,若
为坐标原点,若![]() ,直线
,直线![]() 的一个法向量为
的一个法向量为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是正方形,
是正方形, ![]() .
.
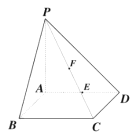
(1)求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD-A1B1C1D1的顶点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA1→A1D1→ ,黄“电子狗”爬行的路线是AB→BB1→ ,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1,2. 第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2; 那么第10次“H扩展”后得到的数列的所有项的和为( )
A.88572B.88575C.29523D.29526
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,短轴的一个端点
,短轴的一个端点![]() 到
到![]() 的距离等于焦距.
的距离等于焦距.
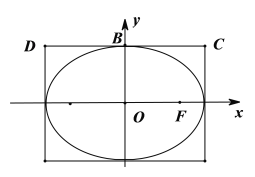
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 、
、![]() 是四条直线
是四条直线![]() ,
,![]() 所围成的矩形在第一、第二象限的两个顶点,
所围成的矩形在第一、第二象限的两个顶点,![]() 是椭圆
是椭圆![]() 上任意一点,若
上任意一点,若![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且满足△
,且满足△![]() 与△
与△![]() 的面积的比值为
的面积的比值为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com