【题目】已知 
=（sinx，sin（x﹣ 
））， 
=（sinx，cos（x+ 
）），f（x）= ．
（1）求f（x）的解析式及周期；
（2）求f（x）在x∈[﹣ ， 
]上的值域．
【答案】
（1）解：f（x）=sin2x+sin（x﹣ 
）cos（x+ 
）=sin2x﹣sin2（x- ）
= 
﹣ 
= 
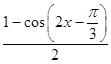[cos（2x﹣ ）﹣cos2x]
= （ 
sin2x﹣ cos2x）= sin（2x﹣ ）．
∴f（x）的周期T= 
=π
（2）解：∵x∈[﹣ ， 
]，∴2x﹣ ∈[﹣ 
， ]，
∴当2x﹣ =﹣ 
时，f（x）取得最小值 
=﹣ ．
当2x﹣ = 时，f（x）取得最大值 
= 
∴f（x）在x∈[﹣ ， ]上的值域是[﹣ ， ]
【解析】（1）利用向量的数量积公式得出f（x），利用二倍角公式，诱导公式及两角和差的三角函数化简；（2）根据x的范围得出2x﹣ 的范围，根据正弦函数的单调性得出f（x）的最值．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知AD=PD，PA=6，BC=8，DF=5，求证： 
（1）直线PA∥平面DEF；
（2）平面DEF⊥平面ABC．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在海岛
上有一座海拔
的山峰，山顶设有一个观察站
，有一艘轮船按一固定方向做匀速直线航行，上午
时，测得此船在岛北偏东
、俯角为
的
处，到
时，又测得该船在岛北偏西
、俯角
为的
处.
（1）求船的航行速度；
（2）求船从
到
行驶过程中与观察站
的最短距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）= 
sin 
，若存在f（x）的极值点x0满足x02+[f（x0）]2＜m2 ， 则m的取值范围是（ ）
A.（﹣∞，﹣6）∪（6，+∞）
B.（﹣∞，﹣4）∪（4，+∞）
C.（﹣∞，﹣2）∪（2，+∞）
D.（﹣∞，﹣1）∪（1，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
， 
为实数， 
， 
为自然对数的底数， 
.
（1）当
， 
时，设函数
的最小值为
，求
的最大值；
（2）若关于
的方程
在区间
上有两个不同实数解，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学初一年级500名学生参加某次数学测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），…，[80,90]，并整理得到如下频率分布直方图：
（1）从总体的500名学生中随机抽取一人，估计其分数小于70的概率；
（2）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
．
（1）判断函数f（x）的奇偶性；
（2）判断并证明f（x）的单调性；
（3）求关于x的不等式f（2x﹣1）+f（x+3）＞0的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
