
【题目】设 ![]() =
= ![]() ,
, ![]() =(4sinx,cosx﹣sinx),f(x)=
=(4sinx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 ![]() 是增函数,求ω的取值范围;
是增函数,求ω的取值范围;
(3)设集合A= ![]() ,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
【答案】
(1)解:f(x)=sin2 ![]() 4sinx+(cosx+sinx)(cosx﹣sinx)
4sinx+(cosx+sinx)(cosx﹣sinx)
=4sinx ![]() +cos2x
+cos2x
=2sinx(1+sinx)+1﹣2sin2x=2sinx+1,
∴f(x)=2sinx+1.
(2)解:∵f(ωx)=2sinωx+1,ω>0.
由2kπ﹣ ![]() ≤ωx≤2kπ+
≤ωx≤2kπ+ ![]() ,
,
得f(ωx)的增区间是 ![]() ,k∈Z.
,k∈Z.
∵f(ωx)在 ![]() 上是增函数,
上是增函数,
∴ ![]()
![]() .
.
∴﹣ ![]() ≥﹣
≥﹣ ![]() 且
且 ![]() ≤
≤ ![]() ,
,
∴ ![]() .
.
(3)解:由|f(x)﹣m|<2,得﹣2<f(x)﹣m<2,即f(x)﹣2<m<f(x)+2.
∵AB,∴当 ![]() ≤x≤
≤x≤ ![]() 时,
时,
不等式f(x)﹣2<m<f(x)+2恒成立,
∴f(x)max﹣2<m<f(x)min+2,
∵f(x)max=f( ![]() )=3,f(x)min=f(
)=3,f(x)min=f( ![]() )=2,
)=2,
∴m∈(1,4).
【解析】(1)通过数量积的计算,利用二倍角公式化简函数的表达式,化为一个角的一个三角函数的形式,即可.(2)结合正弦函数的单调增区间,y=f(ωx)在区间 ![]() 是增函数,说明
是增函数,说明 ![]()
![]() .求出ω的取值范围;(3)简化集合B,利用AB,得到恒成立的关系式,求出实数m的取值范围.
.求出ω的取值范围;(3)简化集合B,利用AB,得到恒成立的关系式,求出实数m的取值范围.
【考点精析】解答此题的关键在于理解正弦函数的单调性的相关知识,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.


科目:高中数学 来源: 题型:
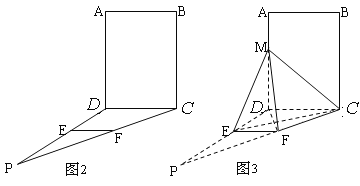
【题目】如图2,四边形![]() 为矩形,
为矩形, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,作如图3折叠,折痕
,作如图3折叠,折痕![]()
![]()
![]() ,其中点
,其中点![]() 分别在线段
分别在线段![]() 上,沿
上,沿![]() 折叠后点
折叠后点![]() 叠在线段
叠在线段![]() 上的点记为
上的点记为![]() ,并且
,并且![]() ⊥
⊥![]() .(1)证明:
.(1)证明: ![]() ⊥平面
⊥平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)在区间上[0,1]的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算出曲线y=f(x)及直线x=0,x﹣1=0,y=0所围成部分的面积S,先产生两组(每组N个)区间[0,1]上的均匀随机数X1 , X2 , X3 , XN和y1 , y2 , y3 , yN , 由此得到N个点(xi , yi)(i=1,2,3N,再数出其中满足yi≤f(xi)(i=1,2,3,N)的点数N1 , 那么由随机方法可以得到S的近似值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保只知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保只是的志愿宣传活动.
名同学到广场参加环保只是的志愿宣传活动.
1)求所抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组的概率;
组的概率;
2)求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,令h(x)=f(x)g(x),且对任意x1 , x2∈(0,+∞),都有 ![]() <0,g(1)=0,则不等式xh(x)<0的解集为 .
<0,g(1)=0,则不等式xh(x)<0的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com