
【题目】新型冠状病毒(SARS-COV-2)是2019年在人体中发现的冠状病毒新毒株,主要通过呼吸道飞沫进行传播,鉴于其特殊的传播途径,某科学医疗机构发现一次性医用口罩起着一定的防护作用一般,口罩在投入市场前需做一系列的检测,其中罩体污点、鼻梁条缺陷、耳绳异常等常规瑕疵肉眼可见,而耳绳尤为关键,会出现耳绳缺失、错位、错熔、漏熔四种情况 .现在生产商大多采用全自动生产线生产口罩,某工厂现有甲(1台本体机拖2台耳带机)和乙(1台本体机拖3台耳带机)两条生产线,已知甲生产线的日产量为7万只,乙生产线的日产量为10万只,生产商为了了解是否有必要更换原有的甲生产线,在设备生产状况相同,不计其他影响的状态下,分别统计了两条生产线生产的1000只口罩的耳绳情况,得到的统计数据如下:
耳绳情况 | 合格 | 缺失 | 错位 | 错熔 | 漏熔 |
甲生产线 | 950 | 9 | 19 | 11 | 11 |
乙生产线 | 900 | 19 | 35 | 25 | 21 |
(1)从乙生产线生产的1000只口罩中随机抽取3只,将合格品的只数记为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)假设口罩的生产成本为0.4元/只,若耳绳发生缺陷时可通过人工修复至合格来挽回损失。耳绳缺失、漏熔时人工修复费为0.01元/只;错位与错熔时需更换耳绳,其中耳绳成本为0.06元/根,人工修复费为0.02元/只.
①以修复费的平均数作为判断依据,判断哪一条生产线在每日生产过程中挽回损失时所需费用较少?
②若经一次检验就合格的口罩,生产商以1元/只的批发价销售给市场,经人工修复的打八折出售。以该工厂的日平均收入为依据分析该生产商是否有必要更换甲生产线?
【答案】(1)见解析;
(2)①甲生产线在每日生产过程中挽回损失时所需费用较少;②有必要更换甲生产线
【解析】
(1)求乙生产线的合格频率,以频率为概率,乙生产线合格的概率为![]() ,不合格的概率为
,不合格的概率为![]() ,随机变量的取值为:
,随机变量的取值为:![]() ,分别用二项分布求概率即可,列出分布列和求数学期望.
,分别用二项分布求概率即可,列出分布列和求数学期望.
(2)①甲生产线1000产品中,不合格为50件.求缺失、漏熔共有20件,按照人工修复费为0.01元/只;错位与错熔时需更换耳绳的共有30件,人工修复费共为0.08元/只,求出总修复费用,再求平均数即可.乙生产线同理可得.比较大小即可.
②甲、乙日平均收入为:合格产品的收入+不合格产品的收入-不合格产品的修复费用.
得出甲收入![]() ,乙收入
,乙收入![]() ,乙比甲多11682,所以有必要更换甲生产线.
,乙比甲多11682,所以有必要更换甲生产线.
(1)乙生产线产品合格的频率为:![]()
以频率为概率,乙生产线合格的概率为![]() ,不合格的概率为
,不合格的概率为![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
(2)
①甲生产线修复费的平均数为: ![]()
乙生产线修复费的平均数为: ![]()
甲生产线在每日生产过程中挽回损失时所需费用![]() 元
元
乙生产线在每日生产过程中挽回损失时所需费用![]() 元
元
所以,甲生产线在每日生产过程中挽回损失时所需费用较少.
②甲日平均收入: ![]()
乙日平均收入:
![]()
乙比甲多11682,所以有必要更换甲生产线.


科目:高中数学 来源: 题型:
【题目】2020年5月17日晚“2019年感动中国人物名单揭晓”,中国女排位列其中,在感动中国的舞台上,她们的一句“我们没赢够”,再次鼓舞中国人民中国之光——中国女排,一次次在逆境中绝地反击,赢得奥运冠军,“女排精神”也是我们当前处于“新冠”逆境中的高三学子们学习的榜样,前进的动力.一次比赛中,中国女排能够闯入决赛的概率为0.8,在闯入决赛条件下中国女排能够获胜的概率是0.9,则中国女排闯进决赛且获得冠军的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟领先他10米,当阿基里斯跑完下一个10米时,乌龟先他1米....所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为0.001米时,乌龟爬行的总距离为( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北极冰融是近年来最引人注目的气候变化现象之一白色冰面融化变成颜色相对较暗的海冰,被称为“北极变暗”现象,21世纪以来,北极的气温变化是全球平均水平的2倍,被称为“北极放大”现象.如图为北极年平均海冰面积(![]() )与年平均
)与年平均![]()
![]() 浓度图.则下列说法正确的是( )
浓度图.则下列说法正确的是( )
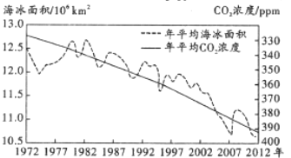
A.北极年海冰面积逐年减少
B.北极年海冰面积减少速度不断加快
C.北极年海冰面积与年平均二氧化碳浓度大体成负相关
D.北极年海冰面积与年平均二氧化碳浓度大体成正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校文科实验班的![]() 名学生期中考试的语文、数学成绩都不低于
名学生期中考试的语文、数学成绩都不低于![]() 分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:
分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
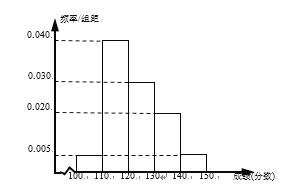
(1)根据频率分布直方图,估计这![]() 名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到
名学生语文成绩的中位数和平均数;(同一组数据用该区间的中点值作代表;中位数精确到![]() )
)
(2)若这![]() 名学生语文成绩某些分数段的人数
名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
从数学成绩在![]() 的学生中随机选取
的学生中随机选取![]() 人,求选出的
人,求选出的![]() 人中恰好有
人中恰好有![]() 人数学成绩在
人数学成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两块相同的正三角形铁皮(如图1,图2),
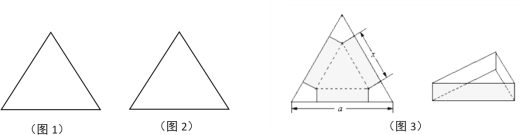
(1)要求用其中一块剪拼成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,
①请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
②试比较你剪拼的正三棱锥与正三棱柱的体积的大小
(2)设正三角形铁皮的边长为![]() ,将正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图3),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?
,将正三角形铁皮的三个角切去三个全等的四边形,再把它的边沿虚线折起(如图3),做成一个无盖的正三角形底铁皮箱,当箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com