
【题目】已知全集U=R,集合A={x|x2+x>0},集合B= ![]() ,则(UA)∪B=( )
,则(UA)∪B=( )
A.[0,2)
B.[﹣1,0]
C.[﹣1,2)
D.(﹣∞,2)
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)若函数 ![]() 在
在 ![]() 上是减函数,求实数
上是减函数,求实数 ![]() 的取值范围;
的取值范围;
(2)是否存在整数 ![]() ,使得
,使得 ![]() 的解集恰好是
的解集恰好是 ![]() ,若存在,求出
,若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:|x﹣a|<3(a为常数);q:代数式 ![]() 有意义.
有意义.
(1)若a=1,求使“p∧q”为真命题的实数x的取值范围;
(2)若p是q成立的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )

A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 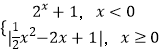 ,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
A.[6,11]
B.[3,11]
C.(6,11)
D.(3,11)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com