
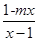 (a>0且a≠1)的图像关于原点对称
(a>0且a≠1)的图像关于原点对称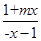 +loga
+loga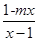 ="0 " ………………………….1分
="0 " ………………………….1分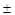 1 …………….3分
1 …………….3分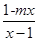 =-1<0 舍去 ∴ m=-1 ……………….4分
=-1<0 舍去 ∴ m=-1 ……………….4分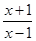
 任取1<x1<x2
任取1<x1<x2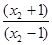 - loga
- loga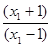 = loga
= loga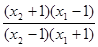
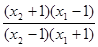 <1
<1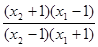 >0,∴f(x2) > f(x1),此时f(x)为增函数…7
>0,∴f(x2) > f(x1),此时f(x)为增函数…7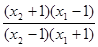 <0,∴f(x2)< f(x1) 此时为减函数。.8分
<0,∴f(x2)< f(x1) 此时为减函数。.8分 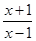 >0有x<-1或x>1∴(t,a)
>0有x<-1或x>1∴(t,a) 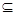 (1,+∞) …………………………..9分
(1,+∞) …………………………..9分 ,且
,且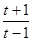 →+∞,∴t="1" ……………12分
→+∞,∴t="1" ……………12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
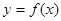 在定义域内单调,且用二分法探究知道
在定义域内单调,且用二分法探究知道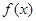 在定义域内的零点同时在
在定义域内的零点同时在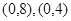 ,
,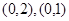 内,那么下列命题中正确的是( )
内,那么下列命题中正确的是( )A.函数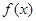 在区间 在区间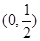 内有零点 内有零点 | B.函数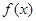 在区间 在区间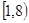 上无零点 上无零点 |
C.函数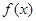 在区间 在区间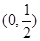 或 或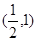 内有零点 内有零点 | D.函数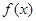 可能在区间 可能在区间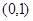 上有多个零点 上有多个零点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com