
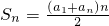 整理为
整理为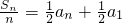 后可知:点
后可知:点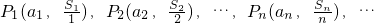 (n为正整数)都在直线
(n为正整数)都在直线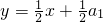 上,类似地,若{an}是首项为a1,公比为q(q≠1)的等比数列,则点P1(a1,S1),P2(a2,S2),…,Pn(an,Sn),…(n为正整数)在直线________上.
上,类似地,若{an}是首项为a1,公比为q(q≠1)的等比数列,则点P1(a1,S1),P2(a2,S2),…,Pn(an,Sn),…(n为正整数)在直线________上.
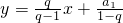 上.
上. =
=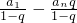 ,
,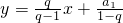 上
上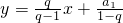 上.
上.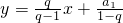 .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com