【题目】体育测试成绩分为四个等级：优、良、中、不及格.某班50名学生参加测试结果如下：
等级 | 优（86～100分） | 良（75～85分） | 中（60～74分） | 不及格（1～59分） |
人数 | 5 | 21 | 22 | 2 |
（1）估计该班学生体育测试的平均成绩；
（2）从该班任意抽取1名学生，求这名学生的测试成绩为“优”或“良”的概率.
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2
ax3（a＞0），x∈R.若对任意的x1∈（2，+∞），都存在x2∈（1，+∞），使得f（x1）
f（x2）=1，则a的取值范围是_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
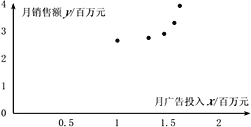
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计，其中i=1，2，3，4，5，对所得数据进行整理，绘制散点图并计算出一些统计量如下：
|
|
|
|
|
|
|
68 | 10．3 | 15．8 | -192．12 | 1．602 | 0．46 | 3．56 |
其中
，i=1，2，3，4，5．
（1）根据散点图判断，
与
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型？(给出判断即可，不必说明理由)
（2）根据（1）的判断结果及题中所给数据，建立y关于x的回归方程，并据此估计月广告投入200万元时的月销售额．
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】6名教师分配到3所薄弱学校去支教，每个学校至少分配一名教师，甲乙两人不能去同一所学校，丙丁两人必须去同一所学校，共有________种分配方案(用数字作答)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，梯形ABCD所在的平面与等腰梯形ABEF所在的平面互相垂直，AB∥CD∥EF，AB⊥AD，CD＝DA＝AF＝FE＝2，AB＝4.
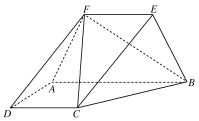
(1)求证：DF∥平面BCE；
(2)求二面角C—BF—A的正弦值；
(3)线段CE上是否存在点G，使得AG⊥平面BCF？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图象关于直线
对称，且图象上相邻两个最高点的距离为
.
（1）求
和
的值；
（2）当
时，求函数
的最大值和最小值；
（3）设
，若
的任意一条对称轴与x轴的交点的横坐标不属于区间
，求c的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（1）求证：
（2）若函数
的图象与直线
没有交点，求实数
的取值范围；
（3）若函数
，则是否存在实数
，使得
的最小值为
？若存在，求出的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
