
【题目】如图,![]() 是底面边长为1的正三棱锥,
是底面边长为1的正三棱锥,![]() 分别为棱长
分别为棱长![]() 上的点,截面
上的点,截面![]() 底面
底面![]() ,且棱台
,且棱台![]() 与棱锥
与棱锥![]() 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

(1)证明:![]() 为正四面体;
为正四面体;
(2)若![]() ,求二面角
,求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(3)设棱台![]() 的体积为
的体积为![]() ,是否存在体积为
,是否存在体积为![]() 且各棱长均相等的直平行六面体,使得它与棱台
且各棱长均相等的直平行六面体,使得它与棱台![]() 有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
(注:用平行于底的截面截棱锥,该截面与底面之间的部分称为棱台,本题中棱台的体积等于棱锥![]() 的体积减去棱锥
的体积减去棱锥![]() 的体积.)
的体积.)
【答案】(1)证明见解析;(2)![]() ;(3)存在,证明见解析.(注:所构造直平行六面体不唯一,只需题目满足要求即可)
;(3)存在,证明见解析.(注:所构造直平行六面体不唯一,只需题目满足要求即可)
【解析】
(1)根据棱长和相等可知![]() ,根据面面平行关系和棱锥为正三棱锥可证得
,根据面面平行关系和棱锥为正三棱锥可证得![]() ,进而证得
,进而证得![]() 各棱长均相等,由此得到结论;(2)取
各棱长均相等,由此得到结论;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据等腰三角形三线合一的性质和线面垂直判定定理可证得
,根据等腰三角形三线合一的性质和线面垂直判定定理可证得![]() 平面
平面![]() ,由线面垂直性质可知
,由线面垂直性质可知![]() ,从而得到
,从而得到![]() 即为所求二面角的平面角;易知
即为所求二面角的平面角;易知![]() ,从而得到
,从而得到![]() ,在
,在![]() 中根据长度关系可求得
中根据长度关系可求得![]() ,从而得到结果;(3)设直平行六面体的棱长均为
,从而得到结果;(3)设直平行六面体的棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]() ,根据正四面体
,根据正四面体![]() 体积为
体积为![]() ,可验证出
,可验证出![]() ;又所构造六面体体积为
;又所构造六面体体积为![]() ,知
,知![]() ,只需满足
,只需满足![]() 即可满足要求,从而得到结果.
即可满足要求,从而得到结果.
(1)![]() 棱台
棱台![]() 与棱锥
与棱锥![]() 的棱长和相等
的棱长和相等
![]()
![]() 平面
平面![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 为正三棱锥
为正三棱锥
![]()
![]()
![]()
![]() 为正四面体
为正四面体
(2)取![]() 的中点
的中点![]() ,连接
,连接![]()
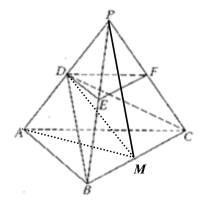
![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 为二面角
为二面角![]() 的平面角
的平面角
由(1)知,![]() 各棱长均为
各棱长均为![]()
![]()
![]() 为
为![]() 中点
中点 ![]()
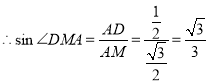
![]()
即二面角![]() 的大小为:
的大小为:![]()
(3)存在满足题意的直平行六面体,理由如下:
棱台![]() 的棱长和为定值
的棱长和为定值![]() ,体积为
,体积为![]()
设直平行六面体的棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]()
则该六面体棱长和为![]() ,体积为
,体积为![]()
![]() 正四面体
正四面体![]() 体积为:
体积为:![]()
![]()
![]()
![]() 时,满足要求
时,满足要求
故可构造棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]() 的直平行六面体即可满足要求
的直平行六面体即可满足要求


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为![]() ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀, 授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为![]() 、
、![]() 、
、![]() ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上![]() 件产品作为样本算出他们的重量(单位:克)重量的分组区间为
件产品作为样本算出他们的重量(单位:克)重量的分组区间为![]() ,
,![]() ,……
,……![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
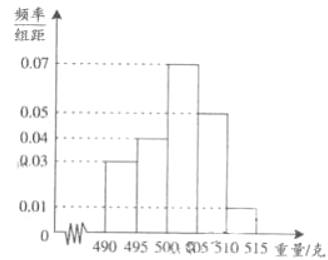
(1)根据频率分布直方图,求重量超过![]() 克的产品数量.
克的产品数量.
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列.
的分布列.
(3)从流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品合格的重量超过
件产品合格的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,不过原点的直线
,不过原点的直线![]() 与椭圆交于A、B两点.
与椭圆交于A、B两点.
(1)求![]() 面积的最大值.
面积的最大值.
(2)是否存在椭圆![]() ,使得对于椭圆
,使得对于椭圆![]() 的每一条切线与椭圆
的每一条切线与椭圆![]() 均相交,设交于A、B两点,且
均相交,设交于A、B两点,且![]() 恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
恰取最大值?若存在,求出该椭圆;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com