
已知多项式f(n)= n5+
n5+ n4+
n4+ n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
(1)0,17(2)见解析
【解析】(1)f(-1)=0,f(2)=17
(2)先用数学归纳法证明,对一切正整数n,f(n)是整数.
①当n=1时,f(1)=1,结论成立.
②假设当n=k(k≥1,k∈N)时,结论成立,即f(k)= k5+
k5+ k4+
k4+ k3-
k3- k是整数,则当n=k+1时,f(k+1)=
k是整数,则当n=k+1时,f(k+1)= (k+1)5+
(k+1)5+ (k+1)4+
(k+1)4+ (k+1)3-
(k+1)3-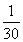 (k+1)
(k+1)
= +
+
+ -
- (k+1)=f(k)+k4+4k3+6k2+4k+1.
(k+1)=f(k)+k4+4k3+6k2+4k+1.
根据假设f(k)是整数,而k4+4k3+6k2+4k+1显然是整数.
∴f(k+1)是整数,从而当n=k+1时,结论也成立.
由①、②可知对一切正整数n,f(n)是整数.
(Ⅰ)当n=0时,f(0)=0是整数
(Ⅱ)当n为负整数时,令n=-m,则m是正整数,由(Ⅰ)知f(m)是整数,
所以f(n)=f(-m)= (-m)5+
(-m)5+ (-m)4+
(-m)4+ (-m)3-
(-m)3- (-m)
(-m)
=- m5+
m5+ m4-
m4- m3+
m3+ m=-f(m)+m4是整数.
m=-f(m)+m4是整数.
综上,对一切整数n,f(n)一定是整数.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用3练习卷(解析版) 题型:解答题
已知函数f(x)= .
.
(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用20练习卷(解析版) 题型:解答题
如图,在四棱锥O ?ABCD中,底面ABCD为菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:(1)平面BDO⊥平面ACO;(2)EF∥平面OCD.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:填空题
已知f(x)=ln(1+x)的定义域为集合M,g(x)=2x+1的值域为集合N,则M∩N=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
已知矩阵M= .
.
(1)求矩阵M的逆矩阵;
(2)求矩阵M的特征值及特征向量.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
形状如图所示的三个游戏盘中(图①是正方形,M,N分别是所在边中点,图②是半径分别为2和4的两个同心圆,O为圆心,图③是正六边形,点P为其中心)各有一个玻璃小球,依次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.

(1)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(2)用随机变量X表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C?PB?A的余弦值..
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:解答题
如图,点P(0,-1)是椭圆C1: =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.

(1)求椭圆C1的方程;
(2)求△ABD面积取最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
在等差数列{an}中,a1=142,d=-2,从第一项起,每隔两项取出一项,构成新的数列{bn},则此数列的前n项和Sn取得最大值时n的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com