
| 日需求量 | 7 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 5 | 7 | 10 | 14 | 10 | 4 |
分析 (Ⅰ)分类求出函数解析式,即可得出利润y关于需求量n的函数解析式;
(Ⅱ)利润在区间[800,900]内,日需求量为10、11、12,其对应的频数分别为14、10、4,即可求出概率.
解答 解:(Ⅰ)当日需求量n≥10时,
利润为y=80×10+(n-10)×40=40n+400; …(2分)
当日需求量n<10时,利润为y=80n-(10-n)×20=100n-200.…(4分)
所以利润y关于需求量n的函数解析式为y=$\left\{\begin{array}{l}{40n+400,n≥10,n∈N}\\{100n-200,n<10,n∈N}\end{array}\right.$…(6分)
(Ⅱ)50天内有5天获得的利润为500元,有7天获得的利润为600元,有10天获得的利润为700元,有14天获得的利润为800元,有10天获得的利润为840元,有4天获得的利润为880元.…(9分)
若利润在区间[800,900]内,日需求量为10、11、12,其对应的频数分别为14、10、4.…(10分)
则利润在区间[800,900]内的概率为$\frac{14+10+4}{50}$=0.56. …(12分)
点评 本题考查了运用概率知识求解实际问题的利润问题,仔细阅读题意,得出有用的数据,理清关系,正确代入数据即可.


科目:高中数学 来源: 题型:选择题
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {0,1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
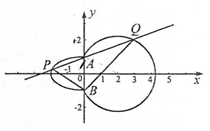 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 水果产量(kg) | 3000 | 4000 |
| 概率 | 0.4 | 0.6 |
| 水果市场价格(元/kg) | 16 | 20 |
| 概率 | 0.5 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 纯虚数 | B. | 实数 | C. | 虚数 | D. | 以上都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com