
已知函数 在
在 上为增函数,且
上为增函数,且 ,
, 为常数,
为常数, .
.
(1)求 的值;
的值;
(2)若 在
在
 上为单调函数,求
上为单调函数,求 的取值范围;
的取值范围;
(3)设 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
如图,二次函数 (
( )的图象与反比例函数
)的图象与反比例函数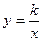 图象相交于点
图象相交于点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在第三象限内,且
在第三象限内,且 的面积为
的面积为 (
( 为坐标原点)
为坐标原点)
① 求实数 的值;
的值;
② 求二次函数 (
( )的解析式;
)的解析式;
③ 设抛物线与 轴的另一个交点为
轴的另一个交点为 ,
, 点为线段
点为线段
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)
某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图一所示;B产品的利润与投资的算术平方根成正比,其关系如图二所示(利润与投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题8分)经过调查发现,某种新产品在投 放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 | 第4天 | 第12天 | 第20天 | 第28天 |
| 价格 (千元) | 34 | 42 | 50 | 34 |
 关于时间
关于时间 的函数表达式(
的函数表达式( 表示投放市场的第
表示投放市场的第 天)
天) 与时间
与时间 的函数关系式为
的函数关系式为 :
: ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,某小区准备在一直角围墙ABC内的空地上植出一块“绿地 ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长)。现规划在
ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长)。现规划在 ABD的内接正方形BGEF内种花,其余地方种草,且把种草的面积
ABD的内接正方形BGEF内种花,其余地方种草,且把种草的面积 与种花的面积
与种花的面积 的比值
的比值 称为“草花比y”
称为“草花比y”
(1)设 ,将y表示成
,将y表示成 的函数关系式。
的函数关系式。
(2)当BE为多长时,y有最小值?最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com