
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅱ)设函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() .证明:
.证明:
(i)![]() ;
;
(ii)对一切![]() 成立.
成立.
【答案】(Ⅰ)两个;(Ⅱ)(i)详见解析;(ii)详见解析.
【解析】
(Ⅰ)分别在![]() 、
、![]() 和
和![]() 三段区间内利用导数求得函数的单调性,结合零点存在定理确定零点个数;
三段区间内利用导数求得函数的单调性,结合零点存在定理确定零点个数;
(Ⅱ)(i)根据(Ⅰ)中结论可知![]() ,
,![]() ,化简
,化简![]() 为
为![]() ,根据
,根据![]() 单调性可证得结论;
单调性可证得结论;
(ii)由(i)的方法可证得![]() ,分别在
,分别在![]() 为奇数和
为奇数和![]() 为偶数两种情况下,采取分组求和的方式,相邻两项配对,即可证得结论.
为偶数两种情况下,采取分组求和的方式,相邻两项配对,即可证得结论.
(Ⅰ)![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() 无零点;
无零点;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
又![]() ,
,![]() ,
,![]() 有唯一零点;
有唯一零点;
当![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 有唯一零点;
有唯一零点;
综上所述:![]() 在
在![]() 有两个零点.
有两个零点.
(Ⅱ)(i)![]() ,
,
由(Ⅰ)知:![]() 在
在![]() 无极值点;在
无极值点;在![]() 有极小值点,即为
有极小值点,即为![]() ,在
,在![]() 有极大值点即为
有极大值点即为![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可知![]() ,
,![]() ,
,
同理在![]() 有极小值点
有极小值点![]() ,…,在
,…,在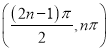 有极值点
有极值点![]() .
.
由![]() 得:
得:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
而![]() ,
,![]() ,故有
,故有![]() ,
,
![]()
![]() 在
在![]() 是增函数,
是增函数,![]() ,
,
即![]() ;
;
(ii)由(i)知:![]() ,
,![]() ,
,
![]() ,
,
由![]() 在
在![]() 递增得:
递增得:![]() ,
,
当![]() 为偶数时,不妨设
为偶数时,不妨设![]() ,从
,从![]() 开始相邻两项配对,每组和均为负值,
开始相邻两项配对,每组和均为负值,
即![]() ,结论成立;
,结论成立;
当![]() 为奇数时,设
为奇数时,设![]() ,
,
![]() ,
,![]() ,
,
从![]() 开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,
开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,
即![]() ,结论也成立.
,结论也成立.
综上,对一切![]() ,
,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题是真命题
”的逆否命题是真命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
C. 若![]() 为真命题,则
为真命题,则![]() 为真命题
为真命题
D. 已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点o为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程是:
为参数),以直角坐标系的原点o为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程是:![]()
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程:
(Ⅱ)点P是曲线C上的动点,求点P到直线l距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学使用某品牌暖水瓶,其内胆规格如图所示.若水瓶内胆壁厚不计,且内胆如图分为①②③④四个部分,它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体.若其中圆台部分的体积为![]() ,且水瓶灌满水后盖上瓶塞时水溢出
,且水瓶灌满水后盖上瓶塞时水溢出![]() .记盖上瓶塞后,水瓶的最大盛水量为
.记盖上瓶塞后,水瓶的最大盛水量为![]() ,
,
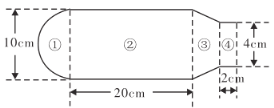
(1)求![]() ;
;
(2)该同学发现:该品牌暖水瓶盛不同体积的热水时,保温效果不同.为了研究保温效果最好时暖水瓶的盛水体积,做以下实验:把盛有最大盛水量![]() 的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温
的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温![]() (单位:℃)与时刻
(单位:℃)与时刻![]() 满足线性回归方程
满足线性回归方程![]() ,通过计算得到下表:
,通过计算得到下表:
倒出体积 | 0 | 30 | 60 | 90 | 120 |
拟合结果 |
|
|
|
|
|
倒出体积 | 150 | 180 | 210 | … | 450 |
拟合结果 |
|
|
| … |
|
注:表中倒出体积![]() (单位:
(单位:![]() )是指从最大盛水量中倒出的那部分水的体积.其中:
)是指从最大盛水量中倒出的那部分水的体积.其中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
令![]() .对于数据
.对于数据![]() ,可求得回归直线为
,可求得回归直线为![]() ,对于数据
,对于数据![]() ,可求得回归直线为
,可求得回归直线为![]() .
.
(ⅰ)指出![]() 的实际意义,并求出回归直线
的实际意义,并求出回归直线![]() 的方程(参考数据:
的方程(参考数据:![]() );
);
(ⅱ)若![]() 与
与![]() 的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且
的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且![]() 取3.14)保温效果最佳?
取3.14)保温效果最佳?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为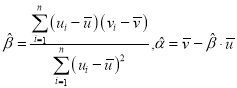 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com