
【题目】互联网![]() 时代的今天,移动互联快速发展,智能手机
时代的今天,移动互联快速发展,智能手机![]() 技术不断成熟,价格却不断下降,成为了生活中必不可少的工具
技术不断成熟,价格却不断下降,成为了生活中必不可少的工具![]() 中学生是对新事物和新潮流反应最快的一个群体之一
中学生是对新事物和新潮流反应最快的一个群体之一![]() 逐渐地,越来越多的中学生开始在学校里使用手机
逐渐地,越来越多的中学生开始在学校里使用手机![]() 手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查
手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查![]() 针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、
针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、![]() 注:图中
注:图中![]() 2,
2,![]() 单位:小时
单位:小时![]() 代表分组为
代表分组为![]() i的情况
i的情况![]()

![]() 求饼图中a的值;
求饼图中a的值;
![]() 假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?
假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?![]() 只需写出结论
只需写出结论![]()
![]() 从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于
从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率,若能,请算出这个概率;若不能,请说明理由
小时的概率,若能,请算出这个概率;若不能,请说明理由
【答案】(1)29%;(2)第4组;(3)若抽取的同学是高二年级的学生,则可以估计这名同学每天平均使用手机小于![]() 小时的概率大约为
小时的概率大约为![]() ,若抽到高一、高三的同学则不能估计.
,若抽到高一、高三的同学则不能估计.
【解析】
![]() 由饼图性质能求出a.
由饼图性质能求出a.
![]() 估计样本中的100名学生每天平均使用手机的平均时间在第4组.
估计样本中的100名学生每天平均使用手机的平均时间在第4组.
![]() 样本是从高二年级抽取的,根据抽取的样本只能估计该校高二年级学生每天使用手机进行娱乐活动的平均时间,不能估计全校学生情况.
样本是从高二年级抽取的,根据抽取的样本只能估计该校高二年级学生每天使用手机进行娱乐活动的平均时间,不能估计全校学生情况.
解:![]() 由饼图得:
由饼图得:![]() .
.
![]() 假设同一组中的每个数据可用给定区间的中点值代替,估计样本中的100名学生每天平均使用手机的平均时间在第4组.
假设同一组中的每个数据可用给定区间的中点值代替,估计样本中的100名学生每天平均使用手机的平均时间在第4组.
![]() 样本是从高二年级抽取的,根据抽取的样本只能估计该校高二年级学生每天使用手机进行娱乐活动的平均时间,不能估计全校学生情况,
样本是从高二年级抽取的,根据抽取的样本只能估计该校高二年级学生每天使用手机进行娱乐活动的平均时间,不能估计全校学生情况,![]() 若抽取的同学是高二年级的学生,则可以估计这名同学每天平均使用手机小于
若抽取的同学是高二年级的学生,则可以估计这名同学每天平均使用手机小于![]() 小时的概率大约为
小时的概率大约为![]() ,若抽到高一、高三的同学则不能估计.
,若抽到高一、高三的同学则不能估计.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,
(a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,![]() )过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
)过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
(1)求椭圆C的方程;
(2)设点![]() ,且MN⊥PQ于N,求直线PQ的方程.
,且MN⊥PQ于N,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法正确的个数是( )
①点F的轨迹是一条线段
②A1F与D1E不可能平行
③A1F与BE是异面直线
④![]()
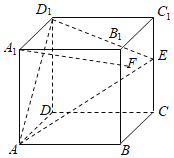
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,射线l:![]() (x≥0),曲线C1的参数方程为
(x≥0),曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的方程为
为参数),曲线C2的方程为![]() ;以原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C3的极坐标方程为
;以原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C3的极坐标方程为![]() .
.
(1)写出射线l的极坐标方程以及曲线C1的普通方程;
(2)已知射线l与C2交于O,M,与C3交于O,N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AB=3,BC=4,E,F分别在线段BC,AD上,EF∥AB,将矩形ABEF沿EF折起,记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.
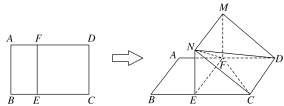
(1)在线段BC是否存在一点E,使得ND⊥FC ,若存在,求出EC的长并证明;
若不存在,请说明理由.
(2)求四面体NEFD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,在亚洲热带地区广泛栽培.槟榔是重要的中药材,在南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周咀嚼槟榔的颗数作为样本绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
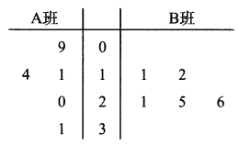
(1)你能否估计哪个班级学生平均每周咀嚼槟榔的颗数较多?
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率;
的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com