
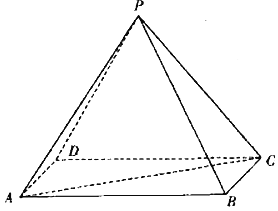
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=2AD=2,∠DAB=60°,PA=PC=2,且平面ACP⊥平面ABCD.
(Ⅰ)求证:CB⊥PD;
(Ⅱ)求二面角C-PB-A的余弦值.
科目:高中数学 来源: 题型:
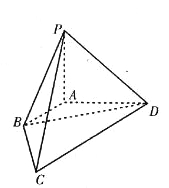
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
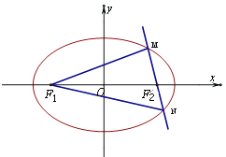
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() (
(![]() )到点
)到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离的差等于1,
轴的距离的差等于1,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于不同于坐标原点
相交于不同于坐标原点![]() 的两点
的两点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机给人们的生活带来便捷,但同时也对中学生的生活和学习造成了严重的影响,某校高一几个学生成立研究性学习小组,就使用手机对学习成绩的影响随机抽取了该校100名学生的期末考试成绩并制成如下的表,则下列说法正确的是( )
成绩优秀 | 成绩不优秀 | 合计 | |
不用手机 | 40 | 10 | 50 |
使用手机 | 5 | 45 | 50 |
合计 | 45 | 55 | 100 |
(附:![]() 列联表
列联表![]() 公式:
公式: ,其中
,其中![]() )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
A.在犯错误的概率不超过0.001的前提下认为使用手机与学习成绩有关.
B.在犯错误的概率不超过0.001的前提下认为使用手机与学习成绩无关.
C.有![]() 的把握认为使用手机对学习成绩无影响.
的把握认为使用手机对学习成绩无影响.
D.无![]() 的把握认为使用手机对学习成绩有影响.
的把握认为使用手机对学习成绩有影响.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某不透明纸箱中共有4个小球,其中1个白球,3个红球,它们除颜色外均相同.
(Ⅰ)一次从纸箱中摸出两个小球,求恰好摸出2个红球的概率;
(Ⅱ)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取4次,记得到红球的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取100次,得到几次红球的概率最大?只需写出结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已数列![]() 的各项均为正整数,且满足
的各项均为正整数,且满足![]() ,又
,又![]() .
.
(1)求![]() 的值,猜想
的值,猜想![]() 的通项公式并用数学归纳法证明;
的通项公式并用数学归纳法证明;
(2)设![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex-alnx(无理数e=2.718…).
(1)若f(x)在(0,1)单调递减,求实数a的取值范围;
(2)当a=-1时,设g(x)=x(f(x)-xex)-x3+x2-b,若函数g(x)存在零点,求实数b的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com