(1)以AB为直径的半圆上,除A、B两点外,另有6个点,又因为AB上另有4个点,共12个点,以这12个点为顶点共能组成多少个四边形?
(2)在角A的一边上有五个点(不含A),另一边上有四个点(不含A),由这十个点(含A)可构成多少个三角形?
(3)设有等距离的3条平行线和另外等距离的4条平行线相交,试问以这些交点为顶点的三角形的个数是多少?
解:(1)由题意知本题需要分类讨论:A、B只含有一个点时,共有2(C36+C26C14)=160个;
既含A又含B时,共有C26=15个;
既不含A也不含B时,共有C410-1-C34C16=185个.
∴共有160+15+185=360个.
(2)由题意知本题可以分类来解,
含A点时,可构成C15C14=20个三角形;
不含A点时,可构成C25C14+C15C24=70个三角形.
故共有20+70=90个三角形.
(3)首先做出从12个点中取3个共有的结果,
注意除了同一平行线上的点不能构成三角形以外,还要注意对角线上的点也不能构成三角形.
共有C312-(C34×3+C33×4+4)=200个.
分析:(1)分类讨论:A、B只含有一个点时,共有2(C36+C26C14),既含A又含B时,共有C16个,既不含A也不含B时,共有C410-1-C34C16个,根据分类计数原理得到共有的个数.
(2)本题可以分类来解,当所取得三个点含A点时,可构成C15C14个三角形,当所取得三个点不含A点时,可构成C25C14+C15C24个三角形,根据分类计数原理得到结果.
(3)做出从12个点中取3个共有的结果,注意除了同一平行线上的点不能构成三角形以外,还要注意对角线上的点也不能构成三角形.用所有的结果减去不合题意的结果,得到共有C312-(C34×3+C33×4+4)个.
点评:本题考查排列组合的实际应用,考查计数原理的应用,考查构成三角形的条件,是一个综合题目,注意做题时做到不重不漏.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案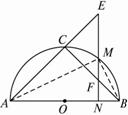
![]() x对称?若存在,请求出a的值;若不存在,请说明理由.
x对称?若存在,请求出a的值;若不存在,请说明理由.