
 ,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________ 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:解答题
 (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2. ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
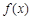 的定义域为
的定义域为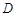 ,若存在非零实数
,若存在非零实数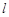 使得对于任意
使得对于任意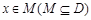 ,有
,有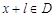 ,且
,且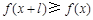 ,则称
,则称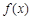 为
为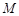 上的
上的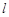 高调函数.如果定义域为
高调函数.如果定义域为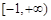 的函数
的函数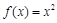 为
为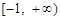 上的
上的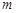 高调函数,那么实数
高调函数,那么实数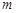 的取值范围是 .如果定义域为
的取值范围是 .如果定义域为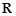 的函数
的函数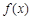 是奇函数,当
是奇函数,当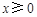 时,
时,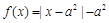 ,且
,且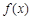 为
为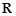 上的4高调函数,那么实数
上的4高调函数,那么实数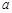 的取值范围是 .
的取值范围是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一 年
种产品进入某商场销售,商场为吸引厂家第一年免收管理费,因此第一 年 种产品定价为每件70元,年销售量为11.8万件. 从第二年开始,商场对
种产品定价为每件70元,年销售量为11.8万件. 从第二年开始,商场对 种产品 征收销售额的
种产品 征收销售额的 的管理费(即销售100元要征收
的管理费(即销售100元要征收 元),于是该产品定价每件比第一年 增加了
元),于是该产品定价每件比第一年 增加了 元,预计年销售量减少
元,预计年销售量减少 万件,要使第二年商场在
万件,要使第二年商场在 种产品经营中收取的管理费不少于14万元,则
种产品经营中收取的管理费不少于14万元,则 的最小值是
的最小值是A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
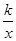 +
+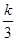 在(1,+∞)上是增函数,则实数k的取值范围是 ( )
在(1,+∞)上是增函数,则实数k的取值范围是 ( )| A.[-2,+∞) | B.[2,+∞) | C.(-∞,-2] | D.(-∞,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com