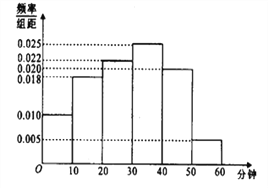
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图，将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.
（Ⅰ）根据已知条件完成下面的
列联表，并据此资料判断你是否有95％以上的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
（参考公式
，其中
.）
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（Ⅱ）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率。
【答案】（Ⅰ）
列联表如下：
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
没有95%的把握认为“体育迷”与性别有关.;（Ⅱ）
.
【解析】试题分析：（1）根据频率分布直方图计算出“体育迷”共计：
名，期中女生：
名；非体育迷：
名，其中女生为
名，男生：
名.填入表格；根据
公式即可求出；（2）由平率分布直方图知，“超级体育迷”为5人，这是一个古典概型的概率问题，分别列出总的基本事件，找出“至少有1名女性观众”的基本事件，然后根据古典概型概率的计算公式算出.
试题解析：（Ⅰ）在抽取的100人中，“体育迷”有25人，从而列联表如下：
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将列联表中的数据代入公式计算，得
.
因为
,则没有95%的把握认为“体育迷”与性别有关.
（Ⅱ）由平率分布直方图知，“超级体育迷”为5人，从而一切可能的结果所组成的基本事件为
，
，
，
，
，
，
，
，
，
.
其中
表示男性，
.
表示女性，
由10个基本事件组成，而且这些基本事件出现是等可能的，
由
表示“任选2人中，至少有1人是女性”这一事件，则
，，，，，，
中有7个基本事件组成，所以
.
阅读快车系列答案科目：高中数学 来源： 题型：
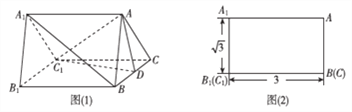
【题目】如图(1)是一个水平放置的正三棱柱
， 
是棱
的中点，正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面
的平面有哪几个(直接写出符合要求的平面即可，不必说明或证明)
(2)求正三棱柱
的体积；
(3)证明： 
平面
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用数字0、2、3、4、6按下列要求组数、计算：
（1）能组成多少个没有重复数字的三位数？
（2）可以组成多少个可以被3整除的没有重复数字的三位数？
（3）求
即144的所有正约数的和.
（注：每小题结果都写成数据形式）
查看答案和解析>>
科目：高中数学 来源： 题型：
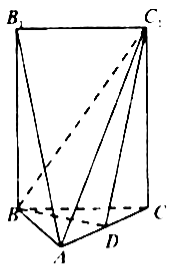
【题目】如图，五面体
中，
，底面
是正三角形，
，四边形
是矩形，二面角
为直二面角．
（1）
在
上运动，当
在何处时，有
平面
，并说明理由；
（2）当
平面
时，求二面角
余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查，随机抽取了60人，作出了他们的月收入频率分布直方图（如图），同时得到了他们月收入情况与赞成人数统计表（如下表）：
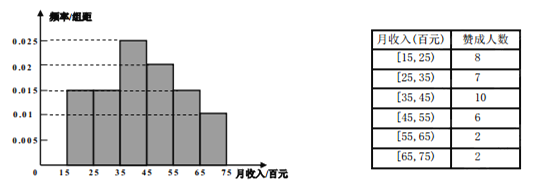
（1）试根据频率分布直方图估计这60人的平均月收入；
（2）若从月收入（单位：百元）在[65，75）的被调查者中随机选取2人进行追踪调查，求2人都不赞成的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂修建一个长方体无盖蓄水池，其容积为6400立方米，深度为4米．池底每平方米的造价为120元，池壁每平方米的造价为100元．设池底长方形的长为x米．
（Ⅰ）求底面积，并用含x的表达式表示池壁面积；
（Ⅱ）怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】三国魏人刘徽，自撰《海岛算经》，专论测高望远。其中有一题：今有望海岛，立两表齐，高三丈，前后相去千步，令后表与前表相直。从前表却行一百二十三步，人目著地取望岛峰，与表末参合。从后表却行百二十七步，人目著地取望岛峰，亦与表末参合。问岛高及去表各几何？ 译文如下：要测量海岛上一座山峰
的高度
，立两根高均为
丈的标杆
和
，前后标杆相距
步，使后标杆杆脚
与前标杆杆脚
与山峰脚
在同一直线上，从前标杆杆脚退行
步到
，人眼著地观测到岛峰，、
、三点共线，从后标杆杆脚退行
步到
，人眼著地观测到岛峰，、
、三点也共线，问岛峰的高度
步． （古制：
步=
尺，
里=
丈=
尺=
步）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
