
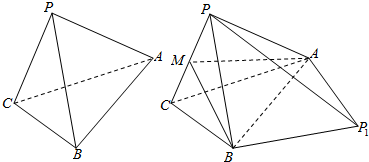
 如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.
如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.分析 (1)连接CP1交AB与于O,连接MO,推导出MO∥PP1,由此能证明直线PP1∥平面MAB.
(2)推导出AM⊥PC,AM⊥BM,由此能证明PC⊥AB.
(3)由已知得AO⊥CP1,AB⊥PC,从而AO⊥平面CPP1,进而∠APO是直线PA与平面P1PC所成角,由此能求出直线PA与平面P1PC所成角的大小.
解答 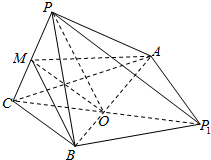 证明:(1)连接CP1交AB与于O,连接MO,
证明:(1)连接CP1交AB与于O,连接MO,
∵AC=AP1=$\sqrt{3}$,CB=BP1=1,∠ACB=∠P1AB=30°,
∴O为CP1中点,
∵点M为PC中点,∴MO∥PP1,
∵MO?平面MAB,PP1?平面MAB,
∴直线PP1∥平面MAB.
(2)∵AP=AC=$\sqrt{3}$,BP=BC=1,M为PC中点,
∴AM⊥PC,AM⊥BM,
∴PC⊥面ABM,AB在面ABM内,
∴PC⊥AB.
解:(3)∵四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,
将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内$\frac{π}{3}$,
O为CP1中点,
∴AO⊥CP1,由(2)知AB⊥PC,
又PC∩CP1=C,∴AO⊥平面CPP1,
∴∠APO是直线PA与平面P1PC所成角,
∵∠ACB=∠P1AB=30°,∴P1O=$\frac{1}{2}A{P}_{\;}$1=$\frac{1}{2}AP$=$\frac{\sqrt{3}}{2}$,
∴$AO=\sqrt{3-\frac{3}{4}}$=$\frac{3}{2}$,
∴sin$∠APO=\frac{AO}{AP}$=$\frac{\frac{3}{2}}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠APO=$\frac{π}{3}$.
∴直线PA与平面P1PC所成角为$\frac{π}{3}$.
点评 本题考查线面平行、线线垂直的证明,考查线面角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{e}{2}$) | B. | (0,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | ($\frac{e}{2}$,$\sqrt{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?
某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com