
【题目】在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。

(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】自2016年底,共享单车日渐火爆起来,逐渐融入大家的日常生活中,某市针对18岁到80岁之间的不同年龄段的城市市民使用共享单车情况进行了抽样调查,结果如下表所示:

(1)采用分层抽样的方式从年龄在![]() 内的人中抽取
内的人中抽取![]() 人,求其中男性、女性的使用人数各为多少?
人,求其中男性、女性的使用人数各为多少?
(2)在(1)中选出![]() 人中随机抽取4人,求其中恰有2人是女性的概率;
人中随机抽取4人,求其中恰有2人是女性的概率;
(3)用样本估计总体,在全市18岁到80岁的市民中抽4人其中男性使用的人数记为![]() ,求
,求![]() 的分布列。
的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
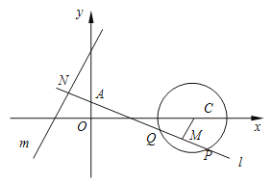
【题目】在平面直角坐标系xOy中,C为直线y=5上的动点,以C为圆心的圆C截y轴所得的弦长恒为6,过原点O作圆C的一条切线,切点为P,则点P到直线3x+4y﹣25=0的距离的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,△ABC和△ABD都是以AB为斜边的直角三角形,AB⊥CD,AB=10,CD=6.
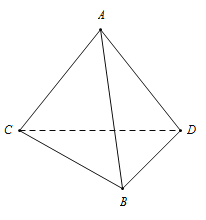
(1)问在AB上是否存在点E,使得AB⊥平面ECD?
(2)如果S△ABC=S△ABD=30,求二面角C﹣AB﹣D的大小.
(3)求三棱锥A﹣BCD体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),平面直角坐标系中,![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,两圆内切于点
,两圆内切于点![]() ,动圆
,动圆![]() 与
与![]() 外切,与
外切,与![]() 内切.
内切.

(1)求动圆![]() 圆心
圆心![]() 的轨迹方程;
的轨迹方程;
(2)如图(2),过![]() 点作
点作![]() 的两条切线
的两条切线![]() ,若圆心在直线
,若圆心在直线![]() 上的
上的![]() 也同时与
也同时与![]() 相切,则称
相切,则称![]() 为
为![]() 的一个“反演圆”
的一个“反演圆”

(ⅰ)当![]() 时,求证:
时,求证:![]() 的半径为定值;
的半径为定值;
(ⅱ)在(ⅰ)的条件下,已知![]() 均与
均与![]() 外切,与
外切,与![]() 内切,且
内切,且![]() 的圆心为
的圆心为![]() ,求证:若
,求证:若![]() 的“反演圆”
的“反演圆”![]() 相切,则
相切,则![]() 也相切。
也相切。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() . 探索
. 探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com