
分析 ①根据含有N个元素的集合的真子集的个数是2N-1,来判断.
②由向量数量积公式进行计算即可.
③由正弦定理可得 a2+b2<c2,则再由余弦定理可得cosC<0,故C为钝角,从而得出结论.
④利用数列的项与和的关系式,求数列的通项.来判断④是否正确.
解答 解:对于①,集合{a1,a2,a3,a4}的真子集的个数为24-1=15,所以①正确;
对于②,由题意知$\overrightarrow{b}$•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=2×4×4cos120°+42=0.∴$\overrightarrow{b}⊥(2\overrightarrow{a}+\overrightarrow{b})$;②正确;
对于③,在△ABC中,若sin2A+sin2B<sin2C,由正弦定理可得 a2+b2<c2,
再由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$<0,故C为钝角,故△ABC是钝角三角形,所以③正确;
对于④,∵{Sn}是等差数列,当n≥2时,an=Sn-Sn-1=d,当n=1时,a1=S1,
∵d、S1不一定相等,∴{an}不一定是常数列.故④不正确.
故答案为:①②③.
点评 本题借助考查命题的真假判断,考查向量的夹角问题.考查正弦定理、余弦定理的应用,数列以及真子集的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
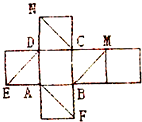 如图是正方体的平面展开图,在这个正方体中:
如图是正方体的平面展开图,在这个正方体中:| A. | ①②③ | B. | ②④ | C. | ②③④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com