
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生M的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
推出的多款健康运动软件中的一款,大学生M的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、
、![]() 步,(说明:“
步,(说明:“![]() ”表示大于或等于0,小于2000,以下同理),
”表示大于或等于0,小于2000,以下同理),![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,
步,![]() 、
、![]() 步,且
步,且![]() 、
、![]() 、
、![]() 三种类别的人数比例为
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
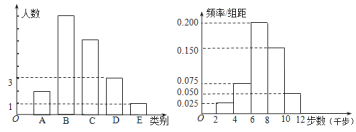
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在![]() 的人数;
的人数;
(Ⅱ)若在大学生![]() 该天抽取的步数在
该天抽取的步数在![]() 的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.
的微信好友中,按男女比例分层抽取6人进行身体状况调查,然后再从这6位微信好友中随机抽取2人进行采访,求其中至少有一位女性微信好友被采访的概率.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)所抽取的40人中,该天行走![]() 步的人数:男12人,女14人,由此能求出400位参与“微信运动”的微信好友中,每天行走
步的人数:男12人,女14人,由此能求出400位参与“微信运动”的微信好友中,每天行走![]() 步的人数.
步的人数.
(Ⅱ)该天抽取的步数在![]() 的人数:男6人,女3人,共9人,再按男女比例分层抽取6人,则其中男4人,女2人,由此能求出其中至少有一位女性微信好友被采访的概率.
的人数:男6人,女3人,共9人,再按男女比例分层抽取6人,则其中男4人,女2人,由此能求出其中至少有一位女性微信好友被采访的概率.
(Ⅰ)由题意,所抽取的40人中,该天行走![]() 步的人数:男12人,女14人,
步的人数:男12人,女14人,
所以400位参与“微信运动”的微信好友中,每天行走![]() 步的人数约为
步的人数约为![]() 人;
人;
(Ⅱ)该天抽取的步数在![]() 的人数中,根据频率分布直方图可知,男生人数所占的频率为
的人数中,根据频率分布直方图可知,男生人数所占的频率为![]() ,所以男生的人数为为
,所以男生的人数为为![]() 人,根据柱状图可得,女生人数为3人,再按男女比例分层抽取6人,则其中男4人,女2人.再从这6位微信好友中随机抽取2人进行采访,基本事件总数
人,根据柱状图可得,女生人数为3人,再按男女比例分层抽取6人,则其中男4人,女2人.再从这6位微信好友中随机抽取2人进行采访,基本事件总数![]() 种,
种,
至少1个女性的对立事件是选取中的两人都是男性,
∴其中至少有一位女性微信好友被采访的概率:![]() .
.


科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面内共始点的三个非零向量,且两两不共线,
是平面内共始点的三个非零向量,且两两不共线,![]() 有下列命题:
有下列命题:
(1)关于![]() 的方程
的方程![]() 可能有两个不同的实数解;
可能有两个不同的实数解;
(2)关于![]() 的方程
的方程![]() 至少有一个实数解;
至少有一个实数解;
(3)关于![]() 的方程
的方程![]() 最多有一个实数解;
最多有一个实数解;
(4)关于![]() 的方程
的方程![]() 若有实数解,则三个向量的终点不可能共线;
若有实数解,则三个向量的终点不可能共线;
上述命题正确的序号是__________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ,回归直线方程
,回归直线方程![]() ,
,
其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: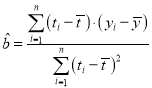 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若以该直角坐标系的原点
为参数),若以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() (其中
(其中![]() 为常数).
为常数).
(1)若曲线![]() 与曲线
与曲线![]() 有两个不同的公共点,求
有两个不同的公共点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,求曲线
时,求曲线![]() 上的点与曲线
上的点与曲线![]() 上点的最小距离.
上点的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
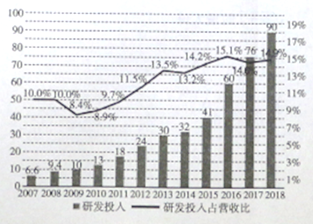
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com