
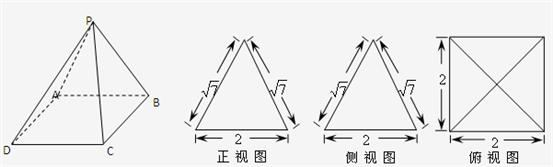
一个多面体的直观图和三视图如下:(其中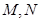 分别是
分别是 中点)
中点)

(1)求证: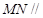 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
(1)见解析;(2) 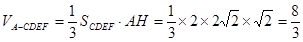 。
。
【解析】
试题分析:(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,那么结合棱柱的性质可知结论成立。
(2)由三视图可知,该多面体是底面为等腰直角三角形的直三棱柱,在直三棱柱中,两个侧面是边长为2的正方形,得到四棱锥的高AE=2,根据四棱锥的体积公式得到结果.
解:
(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,且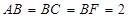 ,
,
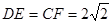 ,∴
,∴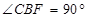 . ---2分
. ---2分
取 中点
中点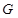 ,连
,连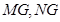 ,由
,由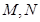 分别是
分别是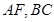 中点,可设:
中点,可设: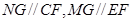 ,
,
∴面 面
面 ∴
∴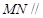 面
面 … ---8分
… ---8分
(2)作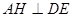 于
于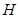 ,由于三棱柱
,由于三棱柱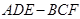 为直三棱柱
为直三棱柱
∴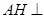 面
面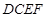 ,
,
且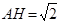 ∴
∴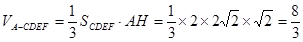 ,---12
,---12
考点:本题主要考查了线面平行的判定定理的运用,以及几何体体积的运算。
点评:解决该试题的关键是能利用三视图还原为几何体,结合几何体的结构特点和公式得到其体积,以及线面的平行的判定。


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
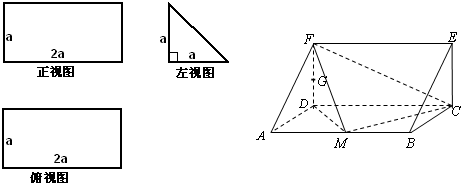
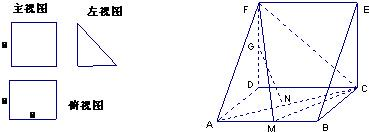 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.查看答案和解析>>
科目:高中数学 来源: 题型:
| DQ | DP |
查看答案和解析>>
科目:高中数学 来源: 题型:

| |DQ| | |DP| |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com