
【题目】在任何![]() 个连续的正整数中,使得必有一数其各位数字之和是7的倍数成立的最小的正整数
个连续的正整数中,使得必有一数其各位数字之和是7的倍数成立的最小的正整数![]() ______.
______.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合,若曲线
轴的非负半轴重合,若曲线![]() 的极坐标系方程为
的极坐标系方程为
![]() ,直线
,直线![]() 的参数方程为
的参数方程为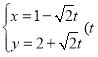 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)设点![]() 直线
直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点, 求
两点, 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
平面直角坐标系![]() 中,射线
中,射线![]() :
:![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() ;以原点为极点,
;以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.曲线
轴的非负半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出射线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知射线![]() 与
与![]() 交于
交于![]() ,
,![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年4月23日我市正式宣布实施“3+1+2”的高考新方案,“3”是指必考的语文、数学、外语三门学科,“1”是指在物理和历史中必选一科,“2”是指在化学、生物、政治、地理四科中任选两科.为了解我校高一学生在物理和历史中的选科意愿情况,进行了一次模拟选科. 已知我校高一参与物理和历史选科的有1800名学生,其中男生1000人,女生800人. 按分层抽样的方法从中抽取了36个样本,统计知其中有17个男生选物理,6个女生选历史.
(I)根据所抽取的样本数据,填写答题卷中的列联表. 并根据![]() 统计量判断能否有
统计量判断能否有![]() 的把握认为选择物理还是历史与性别有关?
的把握认为选择物理还是历史与性别有关?
(II)在样本里选历史的人中任选4人,记选出4人中男生有![]() 人,女生有
人,女生有![]() 人,求随机变量
人,求随机变量![]() 的分布列和数学期望.(
的分布列和数学期望.(![]() 的计算公式见下)
的计算公式见下)![]() ,临界值表:
,临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级的全体学生平均分成![]() 个小组,且每个小组均有
个小组,且每个小组均有![]() 名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的
名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的![]() 名学生中至少有一名男生的概率为
名学生中至少有一名男生的概率为![]() ,则( )
,则( )
A.该班级共有![]() 名学生
名学生
B.第一小组的男生甲被抽去参加社区服务的概率为![]()
C.抽取的![]() 名学生中男女生数量相同的概率是
名学生中男女生数量相同的概率是![]()
D.设抽取的![]() 名学生中女生数量为
名学生中女生数量为![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为![]() .
.
(1)求C的极坐标方程和曲线M的直角坐标方程;
(2)若M与C只有1个公共点P,求m的值与P的极坐标(![]() ,
,![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com