
【题目】设函数f(x)= ![]() +c(e=2.71828…是自然对数的底数,c∈R).
+c(e=2.71828…是自然对数的底数,c∈R).
(Ⅰ)求f(x)的单调区间、最大值;
(Ⅱ)讨论关于x的方程|lnx|=f(x)根的个数.
【答案】解:(Ⅰ)∵f′(x)= ![]() ,解f′(x)>0,得x<
,解f′(x)>0,得x< ![]() ;解f′(x)<0,得x>
;解f′(x)<0,得x> ![]() .
.
∴函数f(x)的单调递增区间为(﹣∞, ![]() );单调递减区间为(
);单调递减区间为( ![]() ,+∞).
,+∞).
故f(x)在x= ![]() 取得最大值,且f(x)max=
取得最大值,且f(x)max= ![]() +c.
+c.
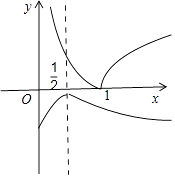
(Ⅱ)函数y=|lnx|,当x>0时的值域为[0,+∞).如图所示:
①当0<x≤1时,令u(x)=﹣lnx﹣ ![]() ﹣c,
﹣c,
c=﹣lnx﹣ ![]() =g(x),
=g(x),
则g′(x)=﹣ ![]() .
.
令h(x)=e2x+x﹣2x2,则h′(x)=2e2x+1﹣4x>0,∴h(x)在x∈(0,1]单调递增,
∴1=h(0)<h(x)≤h(1)=e2﹣1.
∴g′(x)<0,∴g(x)在x∈(0,1]单调递减.
∴c≥g(1)=﹣ ![]() .
.
②当x≥1时,令v(x)=lnx﹣ ![]() ﹣c,得到c=lnx﹣
﹣c,得到c=lnx﹣ ![]() =m(x),
=m(x),
则m′(x)= ![]() >0,
>0,
故m(x)在[1,+∞)上单调递增,∴c≥m(1)=﹣ ![]() .
.
综上①②可知:当c<﹣ ![]() 时,方程|lnx|=f(x)无实数根;
时,方程|lnx|=f(x)无实数根;
当c=﹣ ![]() 时,方程|lnx|=f(x)有一个实数根;
时,方程|lnx|=f(x)有一个实数根;
当c>﹣ ![]() 时,方程|lnx|=f(x)有两个实数根.
时,方程|lnx|=f(x)有两个实数根.
【解析】(Ⅰ)根据题意分析f(x)的导数,讨论f′(x)的正负情况即可得到函数的单调性与最值。(2)由题意转化问题为已知函数在[0,+∞)上的根的情况,逐一讨论去掉绝对值符号再分析导函数的性质,通过单调区间和极值判断各种情况下的根的个数,然后求个情况的并集即可。
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,且∠A=60°,AB=2,E为AB的中点,将四边形EBCD沿DE折起至EDC1B1 , 如图2. 
(Ⅰ) 求证:平面ADE⊥平面AEB1;
(Ⅱ) 若二面角A﹣DE﹣C1的大小为 ![]() ,求三棱锥C1﹣AB1D的体积.
,求三棱锥C1﹣AB1D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题. 
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每 趟最多只能装载40 件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1 , BC1 , AC上的正投影都为三角形时,将它们的面积分别记为S1 , S2 , S3 . 
(i)当BP= ![]() 时,S1S2(填“>”或“=”或“<”);
时,S1S2(填“>”或“=”或“<”);
(ii) S1+S2+S3的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边长分别是a、b、c,且 ![]() ,若将函数f(x)=2sin(2x+B)的图象向右平移
,若将函数f(x)=2sin(2x+B)的图象向右平移 ![]() 个单位长度,得到函数g(x)的图象,则g(x)的解析式为( )
个单位长度,得到函数g(x)的图象,则g(x)的解析式为( )
A.![]()
B.![]()
C.2sin2x
D.2cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn , 满足an+1= ![]() ,n∈N* , 且a2 , a5 , a14构成等比数列.
,n∈N* , 且a2 , a5 , a14构成等比数列.
(1)求数列{an}的通项公式;
(2)若对一切正整数n都有 ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() ,求实数a的最小值.
,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
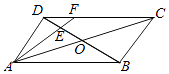
【题目】在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2, ![]() ,∠BAD=45°,则
,∠BAD=45°,则 ![]() =( )
=( )
A.![]()
B.1
C.﹣ ![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=x3+ax2+x在R上是增函数;命题q:若函数g(x)=ex﹣x+a在区间[0,+∞)没有零点.
(1)如果命题p为真命题,求实数a的取值范围;
(2)命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com