
【题目】已知函数![]() 是奇函数
是奇函数
(1)求![]() 的值;
的值;
(2)当![]() 时,求不等式
时,求不等式![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
【答案】(1)k=﹣1;(2)见解析
【解析】
(1)可根据条件得出f(x)是R上的奇函数,从而得出f(0)=0,从而求出k=﹣1;
(2)f(x)=ax﹣a﹣x,求导得出f′(x)=(ax﹣a﹣x)lna,可讨论a,根据导数符号判断f(x)在(﹣1,1)上的单调性,这样根据f(x)是奇函数以及f(x)的单调性即可由不等式f(1﹣m)+f(1﹣2m)<0得出关于m的不等式组,解不等式组即可得出m的范围.
(1)∵f(x)是R上的奇函数,∴f(0)=1+k=0,∴k=﹣1;
(2)f(x)=ax﹣a﹣x,f′(x)=(ax+a﹣x)lna,
∴①0<a<1时,f′(x)<0,f(x)在(﹣1,1)上单调递减,且f(x)是奇函数,
∴由f(1﹣m)+f(1﹣2m)<0得,f(1﹣m)<f(2m﹣1),
∴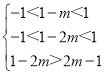 ,解得
,解得![]() ;
;
②a>1时,f′(x)>0,f(x)在(﹣1,1)上单调递增,且f(x)是奇函数,
∴由f(1﹣m)+f(1﹣2m)<0得,f(1﹣m)<f(2m﹣1),
∴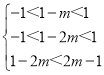 ,解得
,解得![]() ,
,
综上:当0<a<1时,m的取值范围为![]() ,当a>1时,m的取值范围为
,当a>1时,m的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”; 丁说:“
两项作品未获得一等奖”; 丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() 作品 B.
作品 B. ![]() 作品 C.
作品 C. ![]() 作品 D.
作品 D. ![]() 作品
作品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨![]() 年提出了一个著名的猜想:任给一个正整数
年提出了一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘
是奇数,则将它乘![]() 加
加![]() (即
(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到
),不断重复这样的运算,经过有限步后,一定可以得到![]() .对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数
.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数![]() (首项)按照上述规则施行变换后的第
(首项)按照上述规则施行变换后的第![]() 项为
项为![]() (注:
(注:![]() 可以多次出现),则
可以多次出现),则![]() 的所有不同值的个数为( )
的所有不同值的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 及函数
及函数![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)证明:f(x)的图像与g(x)的图像一定有两个交点;
(2)请用反证法证明:![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com