
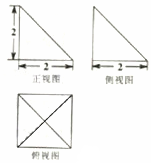
| A. | 4π | B. | 12π | C. | 48π | D. | 6$\sqrt{3}$π |
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | $(2\sqrt{2},8\frac{1}{4})$ | C. | $[3,8\frac{1}{4}]$ | D. | $(2\sqrt{2},3]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{12}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{3}{2}$-$\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
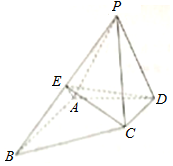 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).| 幸福感强 | 幸福感弱 | 总计 | |
| 留守儿童 | 6 | 9 | 15 |
| 非留守儿童 | 18 | 7 | 25 |
| 总计 | 24 | 16 | 40 |
| P(K2≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com